روغن های PAG از نگاه نزدیک: مطالعه موردی

با سلام و احترام

مقاله حاضر در پاسخ به سوال مطرح شده از طرف یکی از مخاطبین محترم این وبلاگ مهندسی تدوین شده است. علاوه بر این، از آنجا که در حال نگارش مقاله ای طولانی درباره انتخاب روغن گیربکس نیز هستم و این مقاله بخشی از آن را پوشش می دهد، به جهت پرهیز از اطاله کلام، تصمیم به نوشتن این مقاله نسبتا کوتاه گرفتم.

شرح سوال: گیربکسی در یک مجتمع پتروشیمیایی در غرب ایران داریم که از یک هفته پیش برای روغنرسانی بدان از روغن بهران بردبار PG220 استفاده شده است. از زمان شارژ این روغن در مدار روغنرسانی گیربکس (هفت روز پیش)، شاهد سروصدای غیرعادی در زمان عملکرد این تجهیز بودیم تا اینکه پس از هفت روز کارکرد مداوم و جهت بررسی علت سروصدا، درپوش گیربکس را باز کردیم که متوجه جمع شدن قطرات مایعی شبیه آب روی سقف محفظه گیربکس مواجه شدیم. شکل 1 را ببینید.

شکل 1: تشکیل قطرات آب روی سقف محفظه گیربکس

قطرات آب نشان داده شده در شکل 1 پس از چند دقیقه محو شدند. پس از ارسال نمونه روغن درون محفظه گیربکس به آزمایشگاه مشخص شد که روغن درون گیربکس دارای 17,000ppm آب است!

مشکل از کجاست؟ آیا انتخاب بهتری برای این گیربکس وجود دارد؟

این گیربکس دارای دنده های هلیکال بوده و دور ورودی آن برابر 1500rpm و دور خروجی آن 150rpm است. این گیربکس زیر تابش مستقیم نور آفتاب قرار داشته و دمای داخل آن براساس اندازه گیری های انجام گرفته بین 60 تا 70 درجه سلسیوس است. شماتیک مقطع گیربکس در شکل 2 نشان داده شده است.

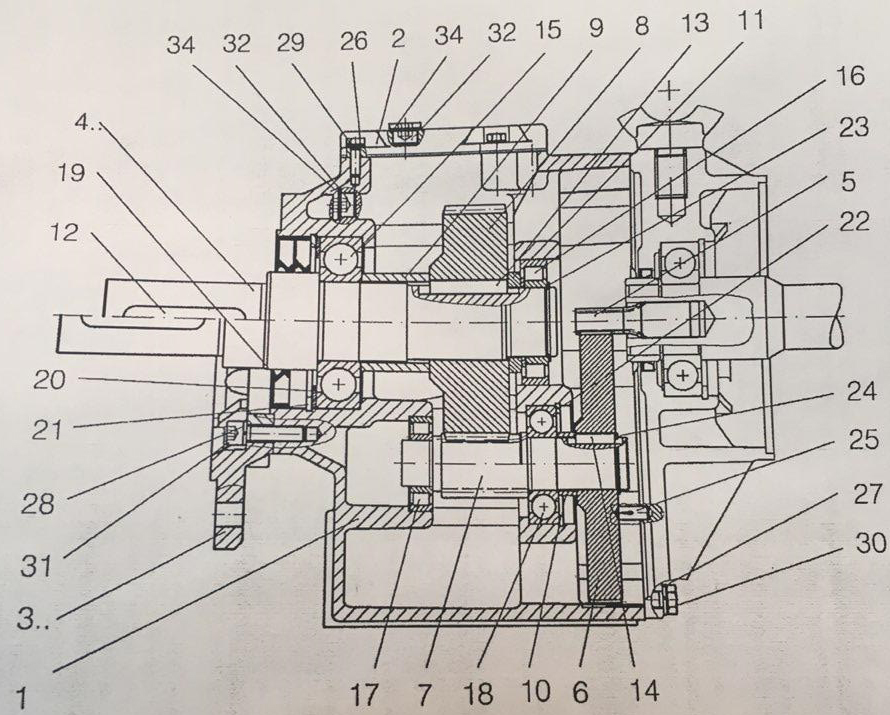
شکل 2: شماتیک مقطع گیربکس

انتخاب روغن PG220 نیز براساس مدارک سازنده تجهیز انجام شده است. شکل 3 را ببینید.

شکل 3.1: تصویری از مدارک سازنده گیربکس (بخش انتخاب روانکار)

شکل 3.2: تصویر دیگری از مدارک سازنده گیربکس (بخش انتخاب روانکار)

همانطور که از شکل های 3.1 و 3.2 مشخص است، می توان برای این گیربکس از روغن های چرخدنده CLP220، PGLP220 یا PGLP460 استفاده کرد که در صورت استفاده از روغن CLP220، زمان تعویض 15000 ساعت و در صورت استفاده از روغن های PGLP220/460 زمان تعویض به 25000 ساعت تغییر می یابد.

البته، براساس شکل 3.2 می توان از گریس Kajo Gear GLP00f نیز برای روانکاری این گیربکس استفاده کرد که دارای درجه قوام NLGI00 بوده و خواص عملکردی آن با کد GP 00 H-20 در استاندارد DIN 51502 تعریف شده است.

پاسخ به این سوال را مستمسکی قرار می دهم برای معرفی روغن های PAG و نگاهی نزدیک به خواص و انواع آنها. این مقاله را که علاوه بر پاسخ به سوال فوق، جنبه آموزشی نیز دارد، با مقدمه ای بر روانکاری گیربکس ها شروع می کنم:

1. مقدمه ای بر روانکاری گیربکس ها

اصولا، هدف از روانکاری چرخدنده ها دو چیز است:

الف) تسهیل لغزش بین دندانه ها از طریق کاهش ضریب اصطکاک μ

ب) محدودسازی روند افزایش دما ناشی از اصطکاک غلتشی و لغزشی (Rolling & Sliding friction) [1]

بمنظور روانکاری گیربکس ها استفاده از طیف متنوعی از روانکارها رایج است که در مورد روغن ها می توان به موارد زیر اشاره کرد:

- روغن های مینرال؛

- هیدروکربن های سینتتیک (پلی آلفا اولفین یا PAOها)؛

- هوموپلیمرهایی مانند پلی آلکیلن گلیکول یا PAGها؛

- استرها؛ و

- روغن های نفتنیک (مانند روغن کلزا یا روغن کرچک) [2]

علاوه بر موارد فوق، استفاده از گریس نیز در روغنرسانی به گیربکس ها و چرخدنده های صنعتی رایج است [1]. اما در چه شرایطی می توان از گریس برای روغنرسانی به یک گیربکس استفاده کرد؟ پاسخ به این سوال در روش روغنرسانی به گیربکس نهفته است.

بطورکلی، برای روغنرسانی به گیربکس ها سه روش وجود دارد:

- روغنرسانی با گریس؛

- روغنرسانی پاششی یا Splash Lubrication (که با عنوان روش حمام روغن یا Oil Bath نیز شناخته می شود)؛ و

- روغنرسانی اجباری (تحت فشار) در یک مدار بسته

فارغ از بهتر یا بدتر بودن، مورد کاربری هر یک از روش های فوق را عواملی چون سرعت مماسی (Tangential Speed) برحسب m/s و سرعت دورانی برحسب rpm تعیین می کنند. در سرعت های پایین، روغنرسانی با گریس انتخاب خوبیست. اما با بالا رفتن سرعت مماسی (یعنی بیش از 3m/s)، استفاده از دو روش روغنرسانی پاششی یا اجباری رواج بیشتری دارد. البته استثنائاتی هم هست. بخصوص در مواردی که سازنده تجهیز ترجیح دهد بدلیل سهولت تعمیر و نگهداری از گریس استفاده شود [1]. جدول 1 اطلاعات بیشتری در این خصوص ارائه می دهد.

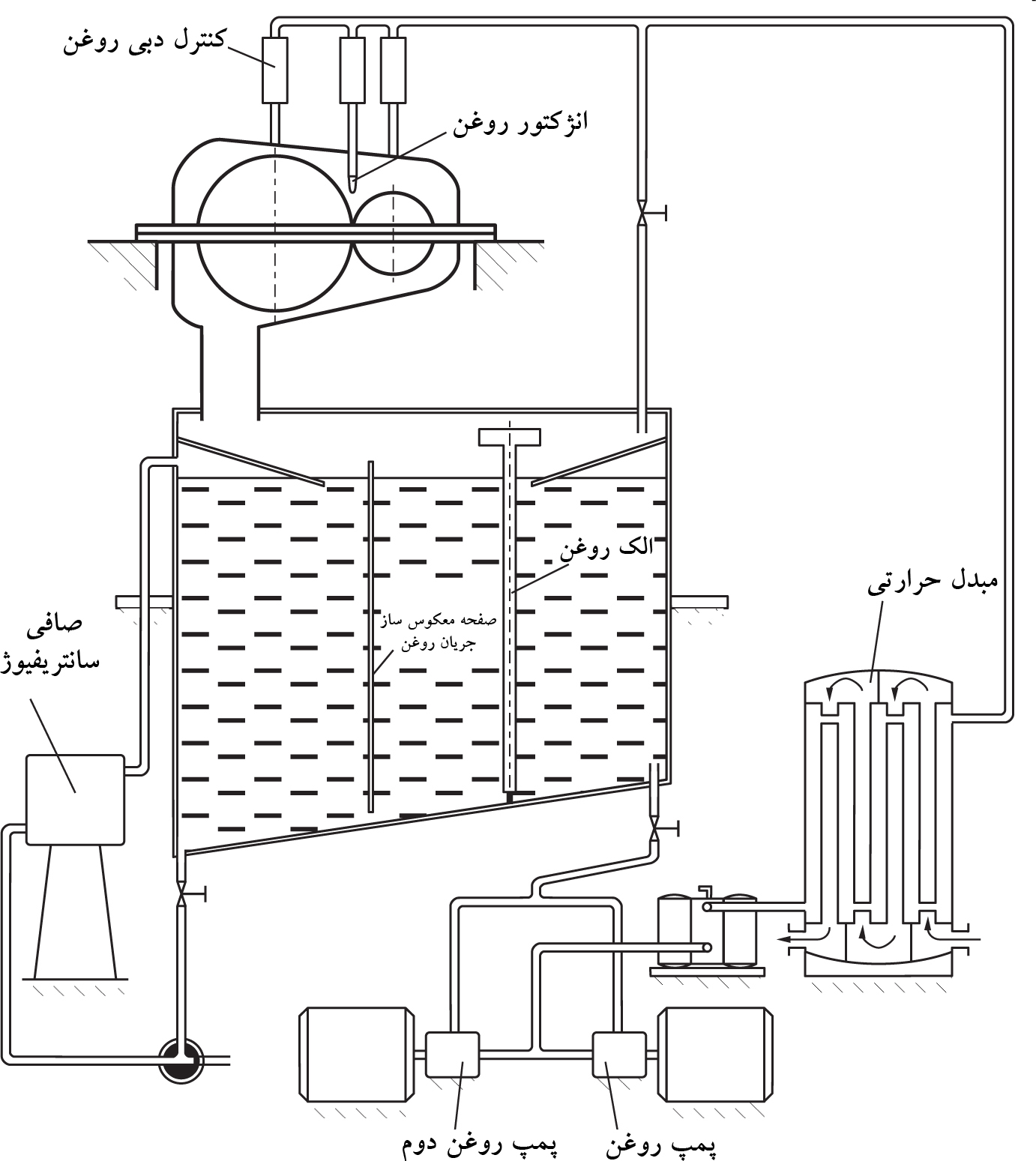
شکل 4: شماتیکی از یک مدار روغنرسانی تیپیکال به یک گیربکس صنعتی [2]

جدول 1.1: حدود مجاز تغییرات سرعت مماسی برای چرخدنده های ساده و مخروطی (Spur & Bevel gears) [1]

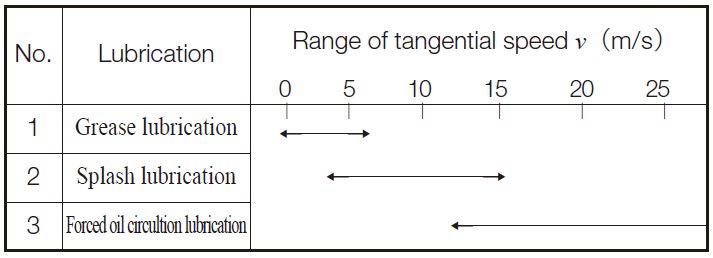
جدول 1.2: حدود مجاز تغییرات سرعت مماسی برای چرخدنده های حلزونی (Worm gears) [1]

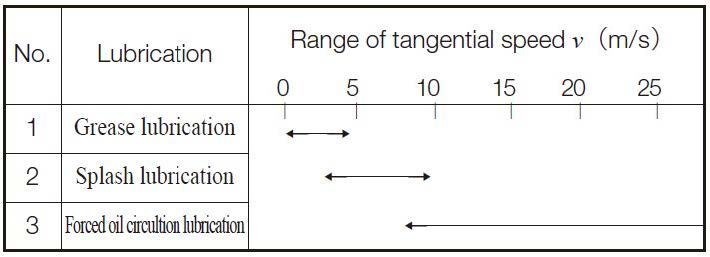
در مورد این گیربکس، با اینکه سرعت مماسی داده نشده، اما با توجه به اینکه دور ورودی گیربکس 1500rpm و دور خروجی آن برابر 150rpm داده شده است، بنابراین نسبت کاهش دور گیربکس روی 10 می ایستد. از این رو، می توان برای این گیربکس براساس داده های جدول 2 نسبت به انتخاب گرید روغن اقدام کرد. جدول 2 را ببینید.

جدول 2: انتخاب روغن برای گیربکس های با محفظه بسته [1]

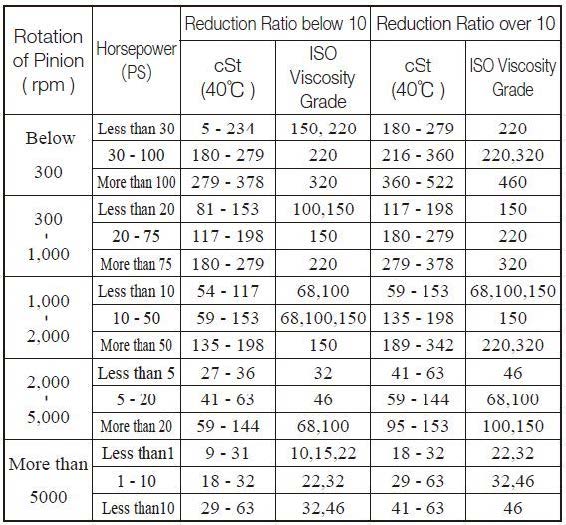
براساس داده های ورودی و اطلاعات جدول 2، ویسکوزیته روغن مصرفی در این گیربکس روی ISO VG 150 می ایستد. اما باید توجه داشت که بهره گیری از داده های جدول 2 دارای محذورات و شرایطی است. اول اینکه این جدول تنها برای چرخدنده های ساده، مارپیچی (Helical gear)، مخروطی، و چرخدنده مخروطی مارپیچ (Spiral Bevel gear) مناسب است که در محفظه بسته قرار داشته و دمای کاری روغن آنها نیز از بازه 10~50°C تجاوز نکند که شرط دوم در مورد این گیربکس صادق نیست. اما، می توان با اعمال درجه حرارت 60~70°C به جریان روغن، میزان ویسکوزیته روغن در آن دما را حساب کرد و با داده های جدول 2 تطبیق داد. ولی چطور می توان ویسکوزیته روغن در دمای کاری گیربکس را حساب کرد؟

برای این منظور، می توان از معادله مک کول-والتر-رایت (McCoul-Walther-Wright) که در مقاله «اثر دما بر ویسکوزیته روغن» تعریف شد و استاندارد ASTM D341 برای محاسبه و پیش بینی ویسکوزیته سینماتیک روغن گیربکس در آن نقطه دمایی خاص (در اینجا: 70°C) بهره جست. برای اینکار، لازم است معادلات (1) و (2) بعنوان صورت لگاریتمیک معادله مک کول-والتر-رایت برای محاسبه ویسکوزیته روغن گیربکس مورد استفاده قرار گیرند (شکل 5 را ببینید). برای بکارگیری معادلات نشان داده شده در شکل 5، لازم است مقدار دو ویسکوزیته سینماتیک روغن گیربکس در دو نقطه دمایی 100 و 40 درجه سلسیوس مشخص باشد. این دو مقدار ورودی به معادلات شکل 5 را، به ترتیب، V1 برای ویسکوزیته سینماتیک روغن گیربکس در 100°C و V2 برای 40°C نامگذاری می کنیم. در مرحله بعد، لازم است دو نقطه دمایی 100 و 40 درجه سلسیوس را برحسب درجه کلوین (°K) بیان کنیم. تبدیل این دو نقطه در سیستم درجه کلوین را به ترتیب t1 (برای 100°C) و t2 (برای 40°C) می نامیم. بدین ترتیب، و با معلوم بودن این چهار مقدار ورودی، دو متغیر α و β قابل محاسبه خواهند بود [3].

شکل 5: معادلات لازم برای محاسبه ویسکوزیته سینماتیک روغن گیربکس در یک نقطه دمایی خاص [3]

در معادلات (1) و (2) که در شکل 5 نشان داده شده اند، متغیرهای ریاضی زیر نماینده این مفاهیم فیزیکی هستند:

- متغیر V(1) بیانگر ویسکوزیته سینماتیک روغن گیربکس در دمای 100°C برحسب mm²/sec؛

- متغیر V(2) نماینده ویسکوزیته سینماتیک روغن گیربکس در دمای 40°C برحسب mm²/sec؛

- متغیر t(1) نشان دهنده دمای نقطه (1) برحسب درجه کلوین است که بصورت زیر قابل محاسبه است:

t(1) = 100°C + 273,15 = 373,15K

- متغیر t(2) نشان دهنده دمای نقطه (2) برحسب درجه کلوین است که بصورت زیر قابل محاسبه است:

t(2) = 40°C + 273,15 = 313,15K

پس از آنکه دو متغیر α و β بدست آمدند، نوبت به محاسبه ویسکوزیته سینماتیک روغن گیربکس در آن نقطه دمایی خاص می رسد. برای اینکار، لازم است مقادیر α و β را به همراه تبدیل آن نقطه دمایی خاص برحسب درجه کلوین وارد معادله شماره (3) کرده و مقدار ویسکوزیته سینماتیک در آن نقطه دمایی خاص را محاسبه کرد. شکل 6 را ببینید:

شکل 6: معادله لازم برای محاسبه ویسکوزیته سینماتیک روغن گیربکس در یک نقطه دمایی خاص [3]

در معادله (3) که در شکل 6 نشان داده شده است، متغیرهای موثر در این معادله عبارتند از:

- متغیر V(s) نماینده ویسکوزیته سینماتیک روغن گیربکس در آن نقطه دمایی خاص برحسب mm²/sec؛

- متغیر t(s) نشان دهنده آن نقطه دمایی خاص که باید ویسکوزیته روغن گیربکس برای آن محاسبه شود برحسب درجه کلوین

نکته: دقت شود که متغیر V(s) ویسکوزیته سینماتیک روغن گیربکس را در آن نقطه دمایی خاص برحسب درجه سلسیوس (°C) بدست می دهد [3].

بعنوان مثال، برای محاسبه ویسکوزیته سینماتیک روغن بهران بردبار PG220 در دمای 70°C (هرچند، دمای 80°C دمای نرمال و معمول برای دندانه چرخدنده هاست [29])، ابتدا با مراجعه به وبسایت شرکت نفت بهران، مقادیر ویسکوزیته سینماتیک این روغن در دو نقطه دمایی 40 و 100 درجه سلسیوس را مشخص می کنیم (شکل 7).

شکل 7: مشخصات عملکردی روغن بهران بردبار PG220 (منبع: شرکت نفت بهران)

ابتدا، برای محاسبه مقدار β، باید مقادیر ویسکوزیته سینماتیک در دو نقطه دمایی 40 و 100 درجه سلسیوس (از شکل 7) را به همراه تبدیل همین نقاط به درجه کلوین در معادله (3) (شکل 6) جایگذاری کرد:

اکنون با داشتن مقدار β، متغیر α حساب می شود. به ترتیب زیر:

 

حال با معلوم بودن مقادیر α و β، و تبدیل مقدار دمای 70 درجه سلسیوس به کلوین، می توان مقدار ویسکوزیته سینماتیک روغن بهران بردبار PG220 را در دمای 70°C محاسبه کرد:

اکنون می دانیم که روغن بهران بردبار PG220 مصرفی در دمای 70 درجه سلسیوس چه ویسکوزیته ای را از خود نشان می داده است. بنابراین، می توان داده های جدول 2 را براساس دمای بالاتری که این گیربکس تجربه می کرده بهبود بخشید (Data Refinement) و نظر سازنده گیربکس در شکل 3.2 مبنی بر امکان استفاده از روغن گیربکس CLP-PG220/460 را صحیح دانست. هرچند، در محاسبه ویسکوزیته سینماتیک روغن CLP-PG220 بهران بردبار شایسته این است که تخمین ویسکوزیته در دمای مورد نظر با استفاده از دو ویسکوزیته سینماتیک در نقاط دمایی 40 و 100 درجه سلسیوس اعلامی از آزمایشگاه انجام شود؛ نه داده های مندرج در کاتالوگ یا وبسایت روغنساز.

اما، به غیر از آنچه که در پاراگراف بالا گفته شد، محاسبه ویسکوزیته روغن مصرفی در گیربکس در یک دمای خاص کاربرد مهمتری نیز دارد. این کاربرد مهمتر چیزی نیست جز تخمین ضخامت فیلم روغن در فضای تبادل تنش بین دو دندانه گیربکس و در نتیجه آن، تعیین رژیم روغنرسانی به دو چرخدنده در آن نقطه دمایی [15]. ولی با این حال، لازمست قبل از آنکه به مبحث نحوه ارتباط ویسکوزیته روغن CLP-PG220 بهران بردبار در دمای 70°C با ضخامت فیلم آن ورود کرده و درباره رژیم های روغنرسانی در چرخدنده های صنعتی صحبت کنیم، بدانیم که در زمان درگیری دو دندانه گیربکس چه اتفاقی برای فیلم روغن محصور بین آنها می افتد. در ابتدای امر، بخش های مختلف ساختار یک چرخدنده ساده را در شکل 8 می بینیم.

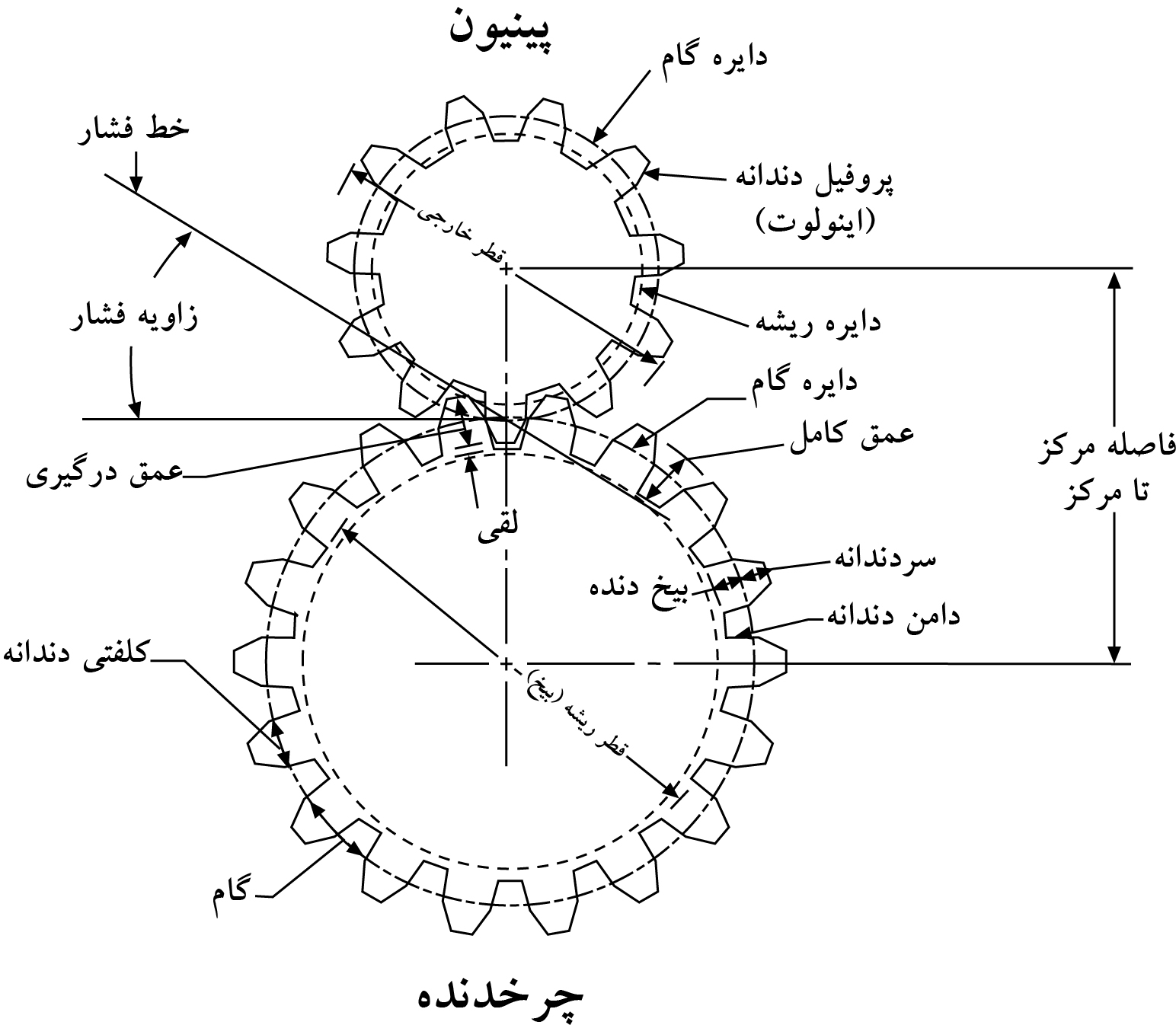
شکل 8: بخش های مختلف تشکیل دهنده یک سیستم چرخدنده و پینیون [21]

حال اگر بخواهیم فضای بین دو دندانه را از نزدیک ببینیم، باید به شکل 9 نگاه کنیم. در شکل 9 الگوی توزیع سه متغیر توصیف کننده شرایط فیلم روغن گرفتار شده در فضای بین دو دندانه یک گیربکس به تصویر کشیده شده است. این سه متغیر عبارتند از: فشار، دما، و ضخامت فیلم روغن.

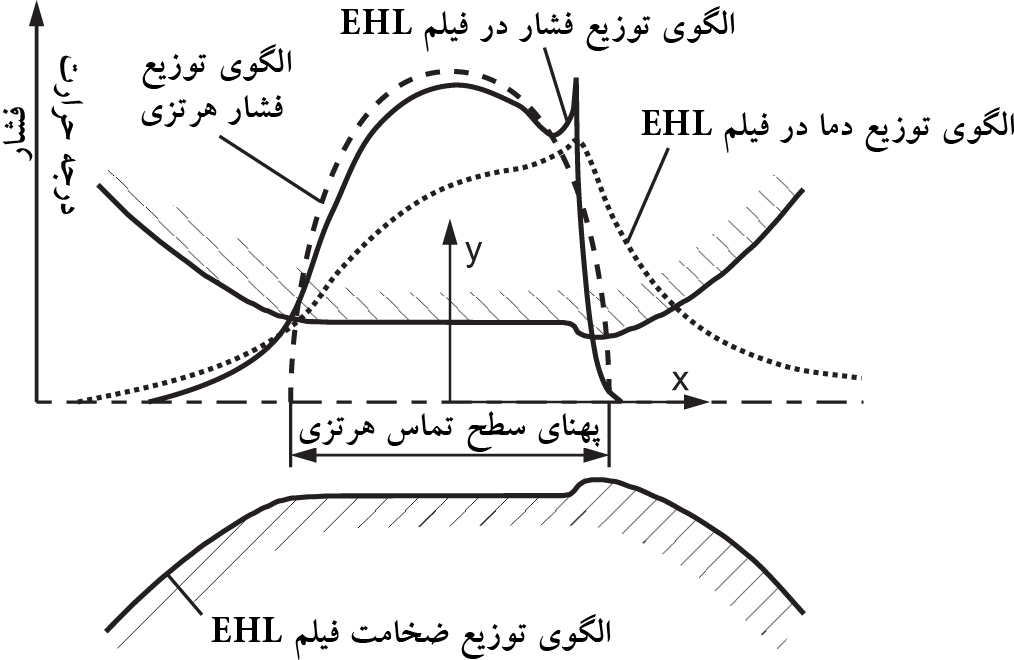
شکل 9: نمودار الگوهای توزیع فشار، دما، و ضخامت فیلم روغن گرفتار شده بین دو دندانه گیربکس [2]

از میان سه عامل فوق، حداقل ضخامتی که فیلم روغن تولیدی خواهد داشت از نقش کلیدی تری بمنظور تخمین رژیم روغنرسانی (بعنوان معیاری برای توصیف شرایط روغنرسانی به فضای بین دو دندانه درگیر) برخوردار است. چراکه فیلم روغن بعنوان حائلی بین دو سطح جامد عمل کرده و از تماس مستقیم دو سطح فلزی با یکدیگر (و در نتیجه، تولید حرارت ناشی از اصطکاک و ساییدگی دو سطح فلزی) جلوگیری می کند. بنابراین، بمنظور تخمین شرایط روغنرسانی به دو دندانه یک گیربکس لازمست حداقل ضخامت فیلم روغنی که انتظار داریم در سطح تماس دو دندانه تشکیل شود را بدانیم.

اما، مشکل اینجاست که حداقل ضخامتی که برای فیلم روغن مفروض محاسبه می شود عددی ثابت نیست و به سادگی با تغییر مشخصات هندسی، دما، بار وارده، و سرعت تغییر می کند. این عدم پایداری در مقدار کمینه ای که از فیلم روغن انتظار داریم ناشی از عدم پایداری ذاتی شرایط لغزش و غلتش (Sliding & Rolling) در محل تماس بین دو دندانه یک گیربکس، اعم از سرعت، هندسه تماس، بار وارده، و حرارت است. بنابراین، طبیعی است که در خط درگیری بین دو چرخدنده شاهد ضخامت های مختلفی از فیلم روغن در نقاط تماس مختلف از دندانه های متفاوت باشیم. این حالت، زمانی بغرنج تر از اینی که هست می شود که بدانیم ضخامت فیلم روغن محاسبه شده برای فضای درگیری بین دو دندانه گیربکس، دیگر برای درگیری دو دندانه بعدی بدرد نمی خورد! چراکه با جداشدن دو دندانه از یکدیگر، فیلم روغن از هم گسیخته شده و حداقل ضخامت فیلم روغن جدید تابع شرایط نسبتا جدیدی از هندسه نقطه تماس، سرعت موضعی، دما، و... خواهد بود.

محاسبه حداقل ضخامت مورد انتظار از فیلم روغن گرفتار در فضای محصور بین دو دندانه گیربکس یکی از موارد مهمی است که در زمان طراحی دندانه ها نیز مورد توجه قرار گرفته و بموجب آن تصویر روشنی از نحوه روغنرسانی به سطوح درگیر دو دندانه در اختیار طراح قرار داده می شود تا نسبت به پیش بینی عمر مفید چرخدنده و سناریوهای خرابی احتمالی، پیش بینی های لازم در دسترس باشد.

بدین ترتیب، طراح می تواند با استناد به ورودی هایی مانند مولفه نیرو، فشار تماسی، و دما و با فرض مقادیر ثابت وابسته به مواد تشکیل دهنده چرخدنده ها و مقادیر مربوط به روانکار (اعم از ویسکوزیته دینامیک آن روغن در نقطه دمایی مفروض از دمای دندانه ها و فرض ضریب فشار α=2000bar) اقدام به محاسبه حداقل ضخامت فیلم روغن بنماید [2].

در فضای نشان داده شده در شکل 9، دو ضخامت برای فیلم روغن متصور است:

الف) حداقل ضخامت (Minimum Film Thickness [7,8,9,11,13,14,17] یا Minimum Lubricant Gap [16]) که با یکی از نشانه های h_min [7,8,9,14,16,17]، h [11]، یا h_m [13] نشان داده می شود و در این مقاله از اینجا به بعد از عبارت h_min برای اشاره بدان بهره خواهیم جست. واحد اندازه گیری h_min در منابع مختلف بصورت in [6,7,11] یا μm [14] قابل بیان است. هرچند ترجیح بسیاری از منابع مهندسی برآنست که از صورت بی بعد (Dimensionless) حداقل ضخامت فیلم روغن که با H_min نشان داده می شود در محاسبات استفاده شود [8,13,16,17,18]؛ و

ب) ضخامت مرکز فیلم روغن (Central Film Thickness) که با h_c نشان داده شده و واحد اندازه گیری آن μm [14] یا in بوده و با h_c [14,16] یا h_cen [17] نشان داده می شود. در منابع مختلف مهندسی، صورت بدون ضخامت مرکز فیلم روغن با Hc نشان داده می شود [13,14,16,18]. در این مقاله، برای اشاره به ضخامت مرکز فیلم روغن از h_c استفاده خواهد شد.

این دو ضخامت به همراه سایر عوامل موثر بر آنها در شکل 10 به تصویر کشیده شده اند.

شکل 10: متغیرهای عامل بر تعیین دو ضخامت حداقل و مرکزی فیلم روغن [16]

تاکنون معادلات مختلفی برای محاسبه h_min پیشنهاد شده است که از جمله معروفترین آنها می توان به Dowson-Higginson (1961)[7,14,22] ، Hamrock-Dowson (1977) [13,16,20]، Moes (1966)، Johnson (1970)، Chittenden et al (1985) [13] و ... اشاره کرد که در این مقاله، بمنظور محاسبه حداقل ضخامت فیلم روغن در منطقه نزدیک به انتهای نقطه تماس دو چرخدنده (همانطور که در شکل 10 نشان داده شده است)، از معادله Dowson-Higginson استفاده می کنیم که دارای دو صورت بوده و صورت اول آن ذیلا نشان داده شده است [7]:

هر یک از پارامترهای نشان داده شده در معادله (1) به شرح زیر تعریف می شوند:

- h_min: حداقل ضخامت فیلم روغن، برحسب in [7] یا μm [14]

- α: ضریب فشار-ویسکوزیته روغن برحسب in²/lbf [6,7,11] یا mm²/N [14]

قبلا در مقاله «اثر فشار بر ویسکوزیته روغن» در همین وبلاگ درباره معادلات مختلف برای محاسبه α صحبت کرده بودیم. یکی از معادلاتی که در آن مقاله بدان اشاره شد، معادله شماره 2 بود:

در معادله فوق، η_p بیانگر ویسکوزیته دینامیک روغن PAG در دمای کاری (در اینجا: 70°C) و فشار p و برحسب Pa.s است. بنابراین، برای محاسبه α ناگزیر از محاسبه η_p هستیم. برای محاسبه η_p از معادله Cameron بهره می گیریم:

در معادله 3، متغیرهای زیر را داریم که هر یک به ترتیب زیر تعیین می شوند:

+ η₀: ویسکوزیته دینامیک در فشار اتمسفریک (یعنی 1bar) و دمای کاری روغن (در اینجا: 70°C)، برحسب Pa.s

بمنظور محاسبه ویسکوزیته دینامیک روغن CLP-PG220 در دمای 70°C و فشار اتمسفریک 1bar، براساس مقاله «اثر دما بر ویسکوزیته روغن» و با فرض ضریب انبساط حرارتی برابر 0.0007 و با معلوم بودن دانسیته روغن در دمای 15°C (براساس جدول مندرج در شکل 7) می توان مقدار دانسیته در دمای 70°C را حساب کرد:

 

بدین ترتیب برای η₀ خواهیم داشت:

 

+ C: عدد ثابت که با استفاده از نمودار شکل 11 انتخاب می شود و با داشتن η₀ و دانستن دمای کاری روغن (70°C) می توان نتیجه گرفت که مقدار C تقریبا برابر با 0.95 خواهد شد.

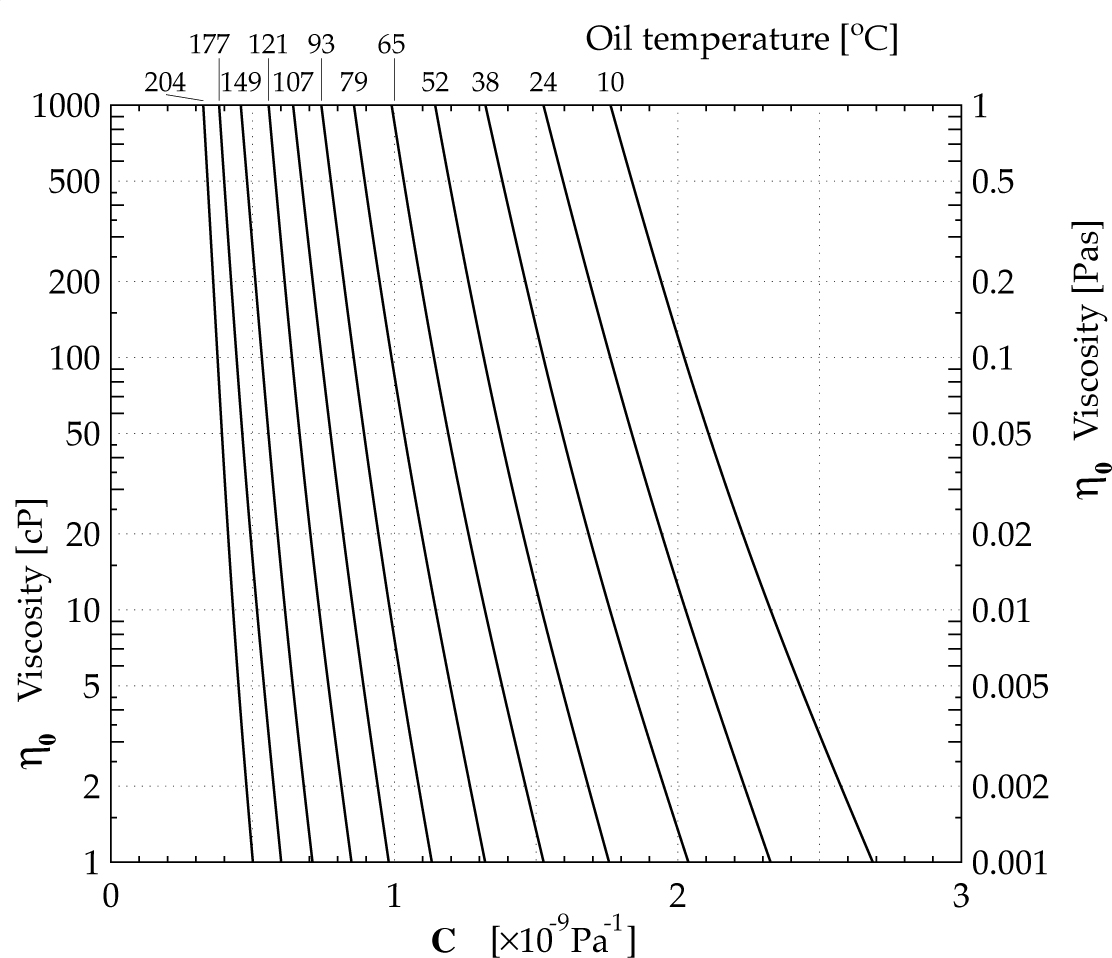
شکل 11: نمودار مرجع تعیین عدد ثابت C برای معادله Cameron (منبع: اثر فشار بر ویسکوزیته روغن)

+ p: فشار نقطه تماس دو دندانه که در اینجا براساس داده های مندرج در [20] برابر 0.94GPa (معادل 9400bar) فرض شده است.

+ n: عدد ثابت که برابر 16 فرض می شود.

بنابراین، برای محاسبه η_p از معادله 3 خواهیم داشت:

 

اکنون که η_p را داریم، برای محاسبه α می توان از معادله 2 اقدام کرد:

 

شایسته اینست که مقدار بدست آمده برای α را با بازه تغییرات معمول آن که در مقاله «اثر فشار بر ویسکوزیته روغن» در همین وبلاگ درج شده بود، مقایسه کنیم. از آن مقاله داشتیم:

بنابراین، مقدار بدست آمده برای α در این مقاله، فعلا در بازه قرار دارد. البته، برای بدست آوردن α روش دیگری نیز موجود است که در مرحله بعدی بدان خواهیم پرداخت که به بررسی صورت دوم معادله Dowson-Higginson می پردازد.

- η: ویسکوزیته مطلق (دینامیک) برحسب lbf/in2 [6,7] یا cP [11] یا m.Pa.s [14]

در خصوص η در معادله 1 لازم به توضیح است که مطابق [11]، این ویسکوزیته دینامیک در دمای محیط است. اما، چون در [7] نمودار تغییرات این ویسکوزیته در برابر دما داده شده است، بنابراین در این مقاله نیز η را ویسکوزیته دینامیک در دمای کاری روغن (یعنی همان η₀ که بالاتر آنرا حساب کردیم) فرض می کنیم.

در عین حال، ویسکوزیته دینامیک در [7] با ₀μ نشان داده شده است که با الهام از [14,16] و در عین حال، مقاله «اثر دما بر ویسکوزیته روغن»، از حرف یونانی η برای اشاره به ویسکوزیته دینامیک در دمای 70°C استفاده شد.

- V_e: سرعت غلتش یا Rolling Velocity [11] یا Entraining Velocity [6,7,13,14] که حاصلجمع دو سرعت غلتشی پینیون و چرخدنده (که به ترتیب با اعداد 1 و 2 مشخص می شوند) و برحسب in/s [7,11] یا m/s [14] بوده و از رابطه زیر حساب می شود:

در معادله 4، متغیر های ρ₁ و ρ₂، به ترتیب، شعاع انحنای ترانسورس پینیون و چرخدنده برحسب in [7,11] یا mm [14]؛ و ω₁ و ω₂ نیز سرعت زاویه ای پینیون و چرخدنده برحسب rad/s [7,14] هستند [7].

البته برای محاسبه سرعت غلتش رابطه ریاضی دیگری نیز موجود است که در مقاله ای جداگانه که مختص موضوع «نحوه محاسبه ضخامت فیلم روغن» نگاشته خواهد شد، به تفصیل بدان خواهیم پرداخت.

در خصوص مقادیر متغیر های ρ₁ و ρ₂، یعنی شعاع انحنا در صفحه ترانسورس پینیون و چرخدنده، ابتدا باید دانست که این دو شعاع انحنا چطور در هندسه گیربکس تعریف می شوند. شکل 12 را ببینید. این شکل خط فشار (Line of Action) یک چرخدنده خارجی (External Gear) را نشان می دهد: همراه با تمامی فواصلی که با نقاط A تا F روی آن مشخص شده اند.

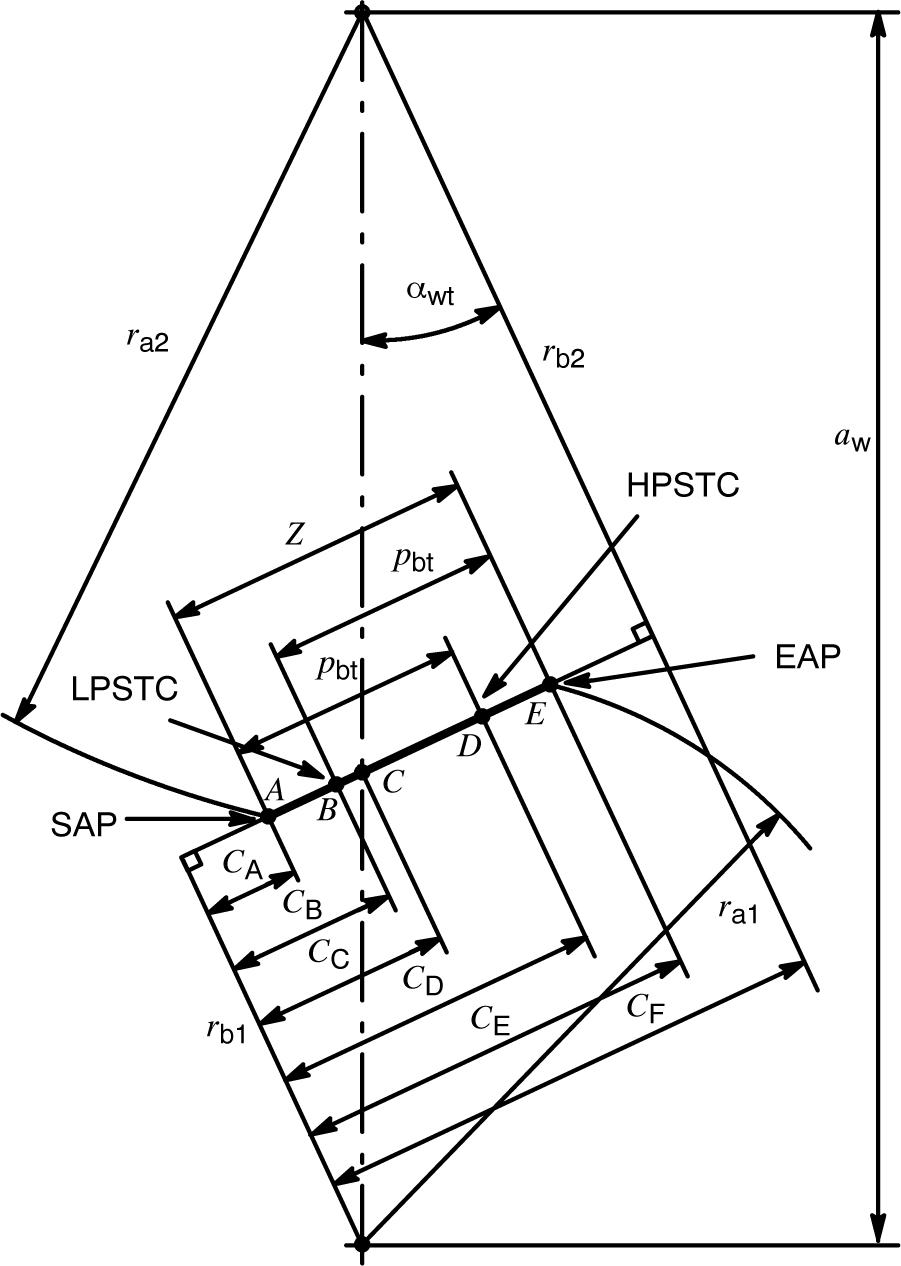
شکل 12: فواصل روی خط فشار یک چرخدنده خارجی [14]

حروف A تا F نماینده نقاط قراردادی و مفروضی هستند که خط فشار یک چرخدنده را به فواصل مختلف تقسیم می کنند. در شکل 12، حروف C_A تا C_F نشاندهنده فاصله نقاط A تا F از نقطه تلاقی پینیون با خط فشار چرخدنده (بعنوان نقطه مرجع یا مرکز دستگاه مختصاتی) هستند.

اکنون که متوجه اهمیت این فواصل قراردادی شدیم، پارامتر جدیدی را با عنوان «زاویه گردش» یا Roll Angle معرفی می کنیم که با حرف یونانی ξ نشان داده شده، برحسب rad بیان شده، و بیانگر زاویه ایست که هر یک از 5 نقطه A تا F در طول خط فشار با شعاع پایه پینیون (r_b1) می سازند. این زاویه از رابطه زیر قابل محاسبه است [14]:

در معادله 5، حرف i بیانگر هر یک از نقاط A، B، C، D، E، یا F است.

حال که دو مفهوم فواصل نقاط فرضی روی خط فشار از نقطه تلاقی پینیون و زاویه ای که هر یک از این فواصل با شعاع پینیون می سازد را دانستیم، می توانیم شعاع انحنای ترانسورس (Transverse Radius of Curvature) که با حرف یونانی ρ نشان داده می شود را تعریف کنیم. شکل 13 را ببینید.

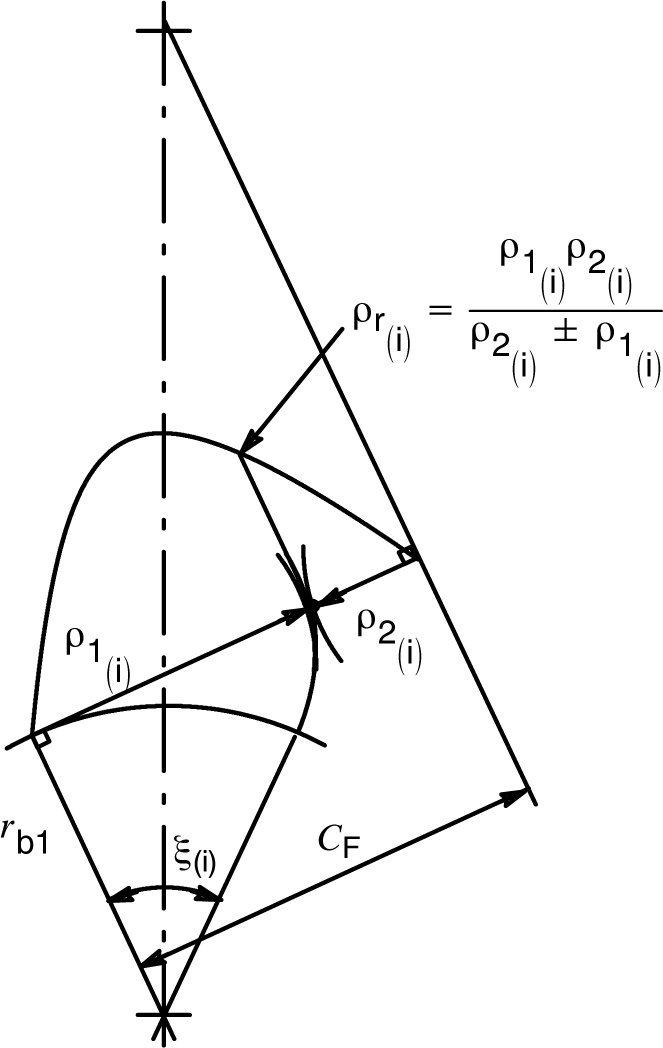
شکل 13: شعاع انحنای ترانسورس در یک چرخدنده خارجی [14]

همانطور که قبلا نیز گفتیم، دو اندیس 1 و 2 بیانگر پینیون و چرخدنده هستند. بنابراین، در شکل 13، دو مشخصه ρ₁ و ρ₂، به ترتیب، نماینده شعاع انحنای پینیون و چرخدنده در صفحه ترانسورس هستند که هر کدام از روابط زیر حساب می شوند [14]:

بنابراین، طبیعی است که مقدار ρ₁ و ρ₂ در طول خط فشار متفاوت باشد.

واضح است که مقادیر لازم برای محاسبه ρ₁ و ρ₂ در اختیار نویسنده این مقاله قرار داده نشده است. از این رو، مقادیری که در Annex D منبع [14] بعنوان مثال در اختیار قرار گرفته را بعنوان مقادیر نمونه انتخاب کرده و محاسبات را با توجه به معادلات 5 تا 7 انجام می دهیم. نتیجه این محاسبات در جدول 3 نشان داده شده است:

جدول 3: محاسبه مقادیر ξ_i، ρ₁، ρ₂، و V_e با استفاده از معادلات 5 تا 7 و با استفاده از مقادیر اولیه اخذ شده از [14]

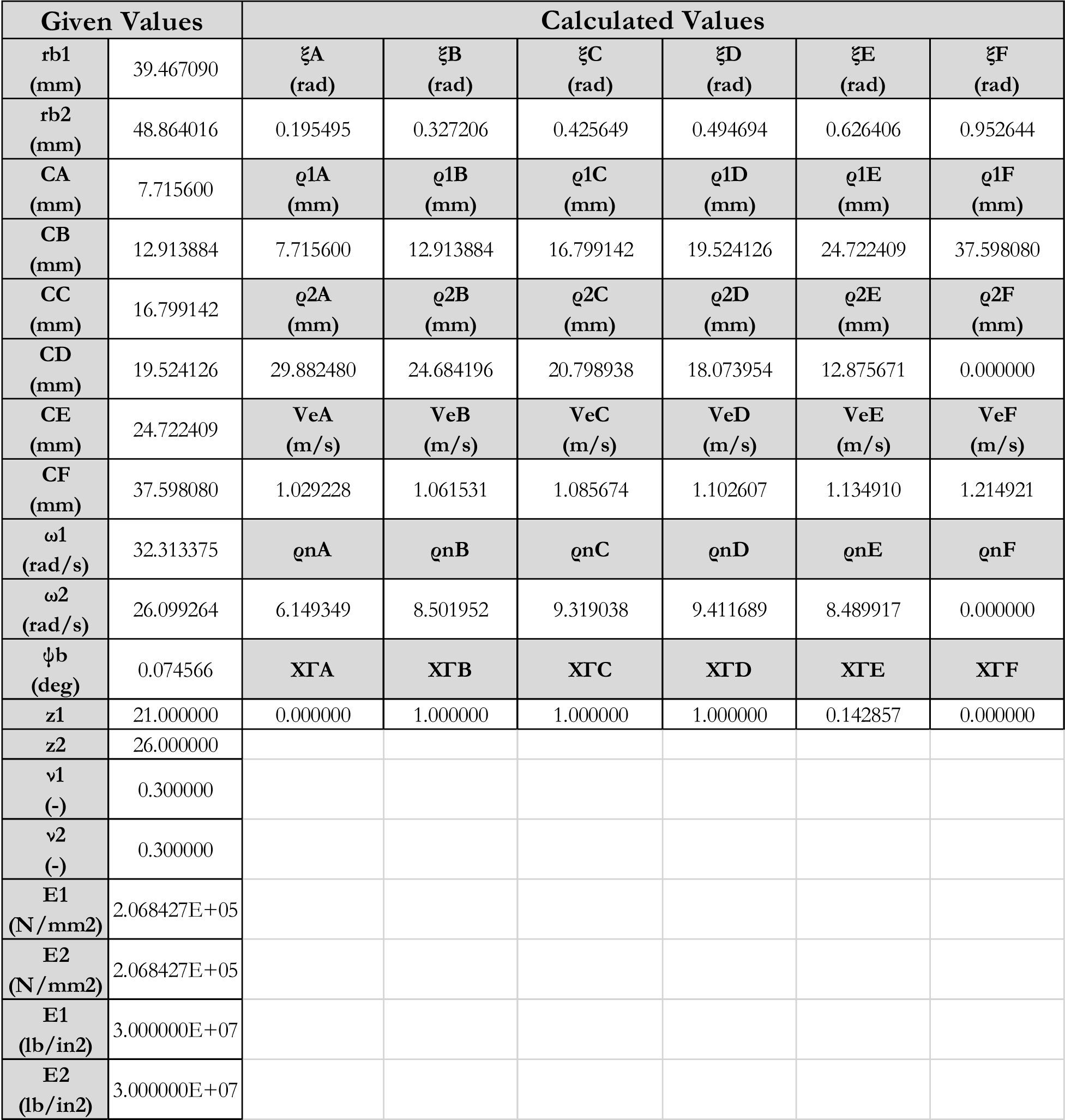
مرحله بعدی به محاسبه دو سرعت زاویه ای پینیون و چرخدنده (یعنی ω₁ و ω₂) اختصاص دارد. سرعت زاویه ای پینیون از رابطه زیر حساب می شود [14]:

در معادله 8، پارامتر n₁ نماینده سرعت پینیون برحسب rpm بوده و با استفاده از داده های Annex D منبع [14] برابر 308.57rpm فرض می شود. بنابراین، سرعت زاویه ای پینیون با توسل به معادله 8 برابرخواهد بود با:

                                                                                                                 

در ادامه، سرعت زاویه ای چرخدنده نیز از رابطه زیر قابل دستیابی است [14]:

حرف u در معادله 9 بیانگر نسبت دنده بوده و از رابطه زیر حساب می شود [14]:

در معادله 10، z₁ نماینده تعداد دندانه های پینیون و z₂ تعداد دندانه های چرخدنده هستند که با استفاده از داده های مندرج در Annex D منبع [14]، مقدار z₁=21 و z₂=26 فرض می شود. بدین ترتیب، برای محاسبه مقدار ω₂ با توسل به معادلات 9 و 10 داریم:

                                                                                                                    

اکنون می توان با استفاده از معادله 4، مقدار سرعت غلتش را حساب کرد. اما، مشکل اینست که مقدار ρ₁ و ρ₂ ثابت نیست و در طول خط فشار تغییر می کند (جدول 3 را ببینید) و همین موضوع مقادیر مختلفی از V_e را بدست می دهد. به ترتیب زیر:

                                                                                                                 

بنابراین، طبیعی است که در طول خط فشار اعداد متفاوتی برای Ve داشته باشیم و اینطور که پیداست، در نقطه F که دورترین نقطه از تلاقی دو دندانه پینیون و چرخدنده است، بیشترین سرعت غلتشی را شاهد هستیم. شکل 14 را ببینید.

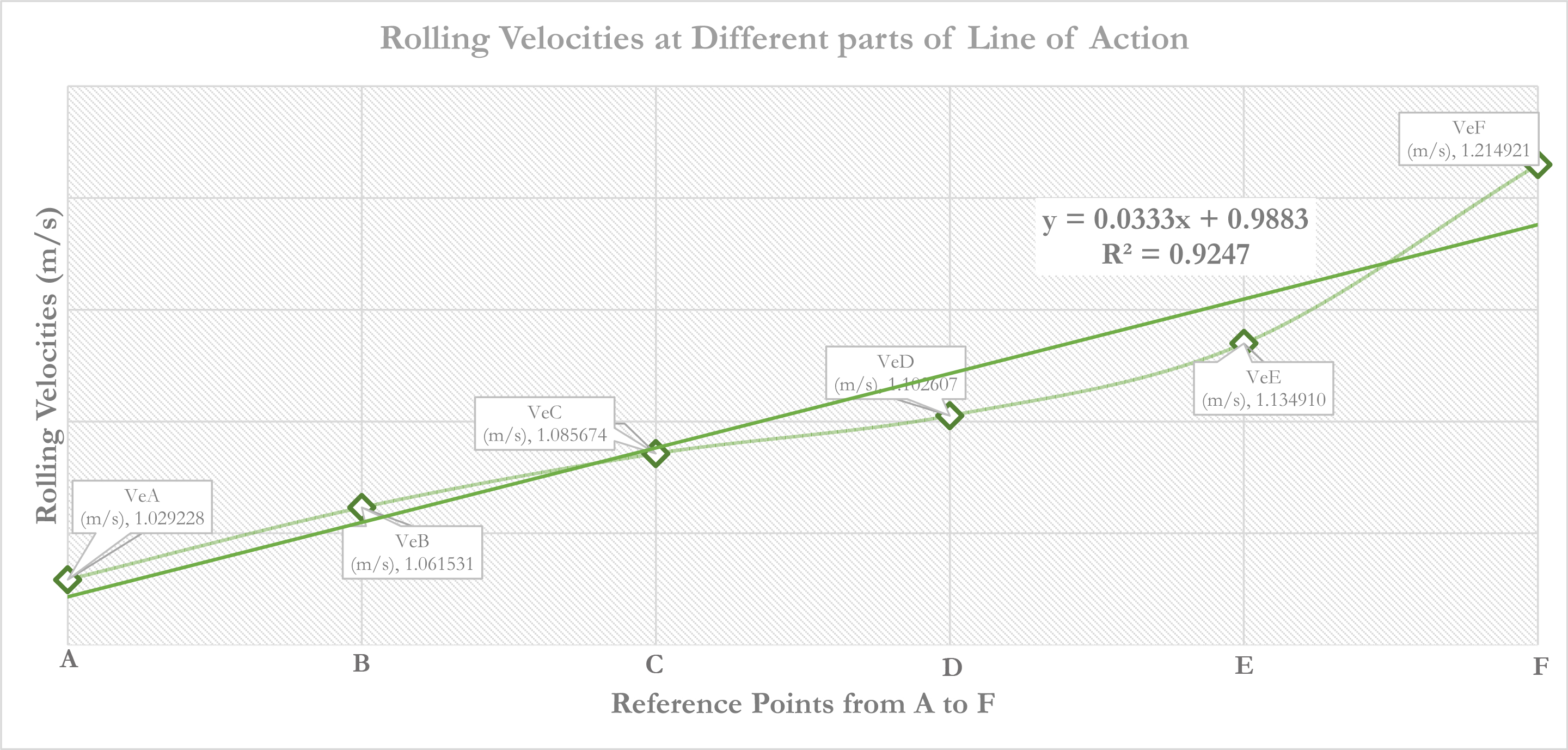
شکل 14: نمودار نمو سرعت غلتشی از نقطه A تا F براساس مقادیر اخذ شده از [14] (خطا: 7.53%)

- ρ_n: شعاع انحنای نسبی در صفحه نرمال برحسب mm [14] یا in [7,11] که از رابطه زیر حساب می شود:

در معادله 11، همانطور که می دانیم، مقادیر ρ1 و ρ2 در طول خط فشار متغیر بوده و نمونه ای از این مقادیر در جدول 3 نشان داده شده است.

نکته: پرانتز مخرج کسر معادله 11 در منابع [7,14] بصورت ρ₂±ρ1 نشان داده شده است که با توجه به مقایسه نتایج محاسبات بدست آمده از Annex D منبع شماره [14]، صورت فوق در این مقاله ترجیح داده شد.

پارامتر ψ_b نیز زاویه پایه مارپیچ یا Helix Base Angle نام داشته و برحسب درجه بیان می شود [7,14]. مقدار این زوایه ψ_b با توسل به معادله زیر قابل محاسبه است [14]:

در معادله 12، پارامترهای p_bn و p_bt، به ترتیب، گام پایه نرمال یا Normal Base Pitch و گام پایه در صفحه ترانسورس یا Transverse Base Pitch بوده که برحسب mm بیان شده و هر یک از روابط زیر قابل محاسبه هستند [14]:

که در معادله 13، m_n نشان دهنده مدول نرمال بوده و از مقادیر داده شده در Annex D منبع شماره [14] برابر با 4mm فرض می شود. پارامتر α_n نیز بیانگر زاویه فشار تولیدی در صفحه نرمال یا Normal Generating Pressure Angle است که با توجه به مقادیر داده شده در Annex D منبع شماره [14] برابر با 20 درجه فرض می شود. بدین ترتیب، p_bn برابر خواهد بود با

                                                                                                               

مقدار p_bt نیز از رابطه زیر حساب می شود:

مقادیر z1 و rb1 را که از قبل می دانیم، از این رو برای محاسبه pbt داریم:

                                                                                                               

بدین ترتیب، و با معلوم شدن مقادیر p_bn و p_bt از معادلات 13 و 14، می توان مقدار ψ_b را با استفاده از معادله 12 حساب کرد:

                                                                                                              

اکنون، با استفاده از معادله 11 می توان مقادیر ρ_n در نقاط A تا F از خط فشار این چرخدنده را حساب کرد که نتایج محاسبه در جدول 3 نشان داده شده است.

- X_Γ: فاکتور تقسیم بار بین چرخدنده و پینیون [7,14]

این فاکتور به نحوه تقسیم بار بین یک جفت دندانه اشاره داشته و از شکل پروفیل دندانه ها تاثیر می پذیرد؛ فارغ از اینکه پینیون عامل حرکت باشد یا چرخدنده. فاکتور تقسیم بار با توسل به یک تابع چندضلعی روی خط فشار و با مقدار بین 1.0 بین دو نقطه B و D تعریف می شود [14]. شکل 15 را ببینید.

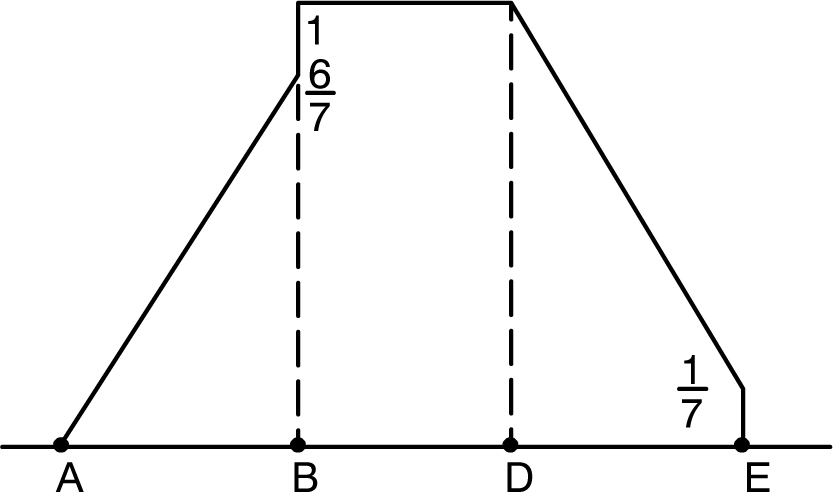
شکل 15: نمودار تقسیم بار بین چرخدنده و پینیون در طول خط فشار [14]

نکته حائز اهمیت اینکه فاکتور تقسیم بار بشدت از وضعیت پرداخت سطح نوک و بیخ دندانه های درگیر (شکل 8) تاثیر پذیرفته و شکل 15 مربوط به حالتی است که نوک و بیخ دندانه ها بمنظور تحمل بار سنگین پرداخت شده و پینیون محرک چرخدنده باشد. بنابراین، مقدار X_Γ در این مقاله از روابط زیر حساب خواهد شد:

بدین ترتیب، مقادیر مختلفی برای X_Γ برای نقاط A تا F بدست می آید که همگی در جدول 3 نشان داده شده اند.

- w_Nr: بارگذاری بازای کوچکترین واحد طول تماس در صفحه نرمال [7,11,14] که با یکی از واحدهای N/mm [14] یا lbf/in [7,11] بیان می شود. بمنظور محاسبه w_Nr فرمول زیر را داریم:

معادله شماره 16 در [11] بصورت زیر و با تعریف «بارگذاری به ازای واحد تماس» آمده است که برای محاسبه آن رابطه زیر برای دندانه های مارپیچ (Helical Gear Teeth) ارائه شده است:

در رابطه شماره 17، W_t بصورت «نیروی مماسی دندانه در نقطه گام» و با واحد اندازه گیری lb و F نیز از رابطه زیر قابل محاسبه است:

که در رابطه فوق، L_min بعنوان «حداقل طول تماس» برحسب mm، زاویه ψ بعنوان «زاویه مارپیچ» برحسب درجه و _nφ بعنوان «زاویه فشار نرمال» و برحسب درجه تعریف می شوند.

اشکال استفاده از رابطه 17 آنست که اولا برای محاسبه W_t رابطه ای داده نشده و ثانیا تاکید شده که این رابطه برای چرخدنده های مارپیچ است که بیشتر جنبه مماسی قضیه برای آنها مهم است. حال آنکه در خصوص w_Nr بیشتر بدنبال جنبه نرمال واحد بارگذاری هستیم. حال، وقتی به [14] نگاهی می اندازیم، رابطه شماره 17 بصورت زیر ظاهر می شود:

رابطه 18 به صورت ریاضی ارائه شده در معادله 16 بیشتر نزدیک است. در خصوص F_wn که بصورت «بار عملکردی نرمال» تعریف می شود، رابطه زیر ارائه شده است:

در معادله شماره 19، دو زاویه α_wn و β_w، به ترتیب، عبارتند از «زاویه فشار عملکردی نرمال» و «زاویه عملکردی مارپیچ» که هر دو برحسب درجه بیان می شوند. متغیر F_t نیز «بار مماسی واقعی» نام داشته، برحسب N بیان شده، و از رابطه زیر قابل محاسبه است:

که در معادله فوق، (F_t)_nom برحسب N بیان شده و «بار مماسی نامی» نام دارد. K_D نیز «ضریب اتلاف بار مرکب یا Combined Derating Factor» نام دارد. این دو متغیر با توسل به روابط زیر قابل محاسبه هستند:

در معادله شماره 22، سه ضریب داریم که همگی از استاندارد ANSI/AGMA 2101-C95 یا نسخه به روز شده آن، ANSI/AGMA 2101-D04 قابل انتخاب و محاسبه هستند (هرچند در این مقاله، این مقادیر از پیوست انتهای [14] بعنوان مثال برداشته شده و داخل محاسبات وارد شده اند). این ضرایب، به ترتیب ظهور در معادله 22، عبارتند از «ضریب بارگذاری بیش از حد یا K_o»، «ضریب توزیع بار یا K_m»، و «ضریب دینامیک یا K_v».

نکته: ضریب K_m که «ضریب توزیع بار» نام دارد در متن استاندارد فوق بصورت K_H ذکر شده است [24].

برگردیم به معادله 21. در این معادله دو متغیر داریم: P که «توان انتقالی یا Transmitted Power» نام داشته و برحسب kW بیان می شود. متغیر ν_t نیز «سرعت خط گام عملکردی یا Operating Pitch Line Velocity» نام داشته و برحسب m/s بیان می شود. سرعت خط گام عملکردی از طریق معادله 23 محاسبه می شود:

دو متغیر حاضر در رابطه شماره 23 به ترتیب عبارتند از:

- ω₁ که «سرعت زاویه ای پینیون» نام داشته و برحسب rad/s بیان می شود. متغیر ω₁ از طریق رابطه شماره 8 قابل محاسبه است و قبلا در این مقاله مقدار آن را داشتیم.

- r_w1 که «شعاع گام عملکردی پینیون» نام داشته و برحسب mm بیان می شود. مقدار r_w1 از معادله شماره 24 قابل محاسبه است:

در رابطه شماره 24، متغیر a_w «فاصله از مرکز عملکردی» نام داشته و برحسب mm بیان می شود. مقدار a_w از [14] انتخاب می شود. u نیز نسبت دنده است که قبلا از رابطه شماره 10 حساب کرده بودیم.

بدین ترتیب، هرچند در [11] برای محاسبه صورت کسر معادله 17 رابطه ای ارائه نشده است، اما، با نگاهی به معادله 19 و جمیع معادلات پس از آن تا معادله 24، می توان نتیجه گرفت که منابع [11] و [14] همگرا هستند. از این رو، می توان صورت معادله 16 را با اندکی تغییر نام در متغیرها، به شرح زیر اصلاح کرد:

متغیرهایی که در معادله 25 مشاهده می کنید، به ترتیب ظهور در معادله، عبارتند از:

- w_Nr: بار واحد نرمال (N/mm یا lbf/in)؛

- F_n: بار عملکردی نرمال (N)؛

- ψ: زاویه مارپیچ عملکردی (درجه)؛

- _nφ: زاویه فشار عملکردی نرمال (درجه)؛ و

- L_min: حداقل طول تماس (mm)

اکنون، با تغییر نام جزیی که در این مقاله و در معادله 16 صورت دادیم تا به معادله 25 برسیم، می توان مقدار w_Nr را حساب کرد. بمنظور محاسبه w_Nr نیاز به مقادیر اولیه ای داریم که از پیوست انتهای [14] انتخاب می شوند در این مقاله. سیر محاسبات تا رسیدن به مقدار w_Nr در شکل 16 نشان داده شده است:

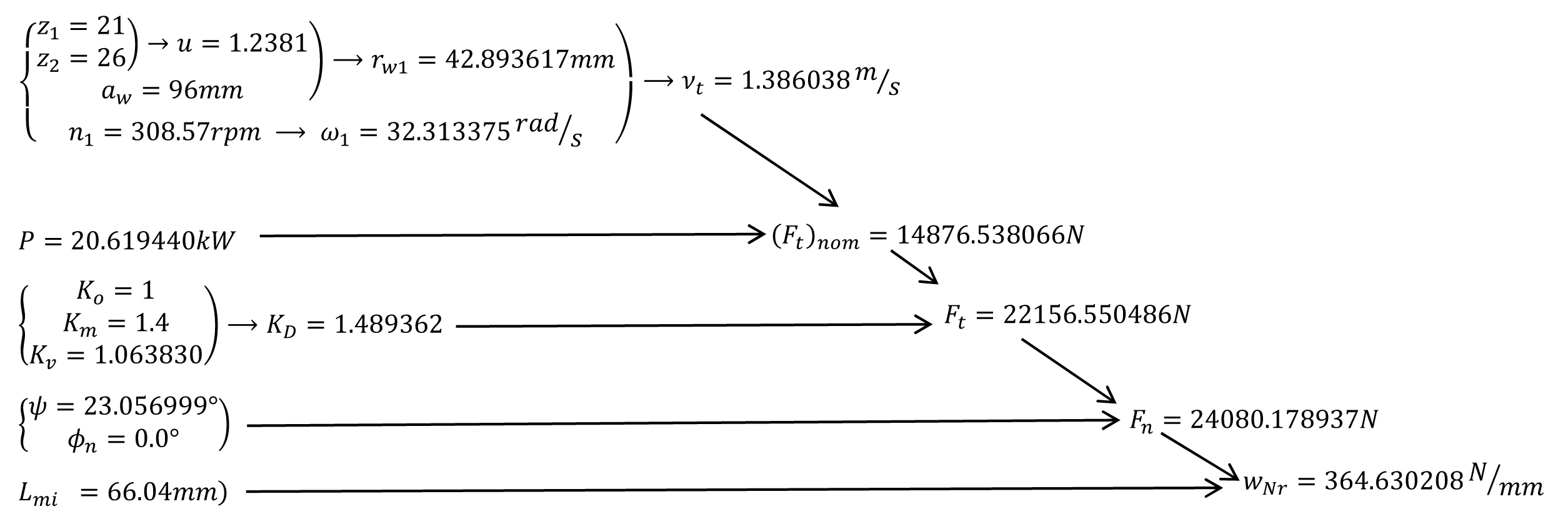
شکل 16: سیر محاسبات از انتخاب مقادیر اولیه تا رسیدن به مقدار محاسباتی برای w_Nr

بدین ترتیب، و براساس سیر محاسبات نشان داده شده در شکل 16، مقدار w_Nr برابر با مقدار زیر محاسبه می گردد:

-         E_r: آخرین متغیر حاضر در معادله 1، E_r است که از آن در برخی منابع با عنوان «مدول الاستیسیته تعدیل یافته» [7,14,22] و در برخی دیگر با عنوان «مدول الاستیسیته موثر» [11] یاد شده است. با نگاهی به چهار منبع [7,11, 14,22]، روابط زیر را برای محاسبه E_r شاهدیم:

در روابط 26 و 27، ν1 و ν2 و E1 و E2، به ترتیب، عبارتند از ضریب پواسون و مدول الاستیسیته پینیون و چرخدنده.

واحد اندازه گیری E_r (یا E’) بصورت N/mm² [14] یا lb/in² [7,11] می باشد.

اکنون، با توجه به اینکه فرمول محاسبه برای Er در [7,14,22] (البته با عنایت به واحد اندازه گیری متفاوت) یکسان است، اقدام به محاسبه مقدار Er براساس هر دو رابطه 26 و 27 می کنیم. نتایج در جدول 4 نشان داده شده است:

جدول 4: محاسبه مقدار E_r (یا E’) با استفاده از معادلات 26 و 27 و با استفاده از مقادیر اولیه اخذ شده از [14]

همانطور که از جدول 4 هویداست، مقدار E_r براساس رابطه شماره 27 حدود 57% نسبت به مقدار E_r محاسبه شده براساس رابطه شماره 26 افزایش می یابد. بر این اساس، می توان نتیجه گرفت که در مورد E_r، سه منبع [7,14,22] در راستای یکدیگر بوده و از این رو، رابطه شماره 26 برای محاسبه E_r انتخاب می شود. بنابراین، در خصوص E_r داریم:

اکنون، از جمیع مقادیر دخیل در معادله Dowson-Higginson یا معادله شماره 1 می توان مقدار h_min برای روغن CLP-PG220 بهران بردبار در دمای 70°C را حساب کرد. البته، قبل از شروع محاسبه باید بدانیم که تمامی واحد های متغیرهای تشکیل دهنده معادله 1 برحسب سیستم ایمپریال هستند (به شرح جدول 5). از این رو، ابتدا باید تمامی مقادیر نشان داده شده در جداول 3 و 4 به سیستم اندازه گیری ایمپریال تبدیل شوند:

جدول 5: واحد های اندازه گیری و مقادیر تبدیل شده برای پارامترهای دخیل در معادله 1 در سیستم ایمپریال

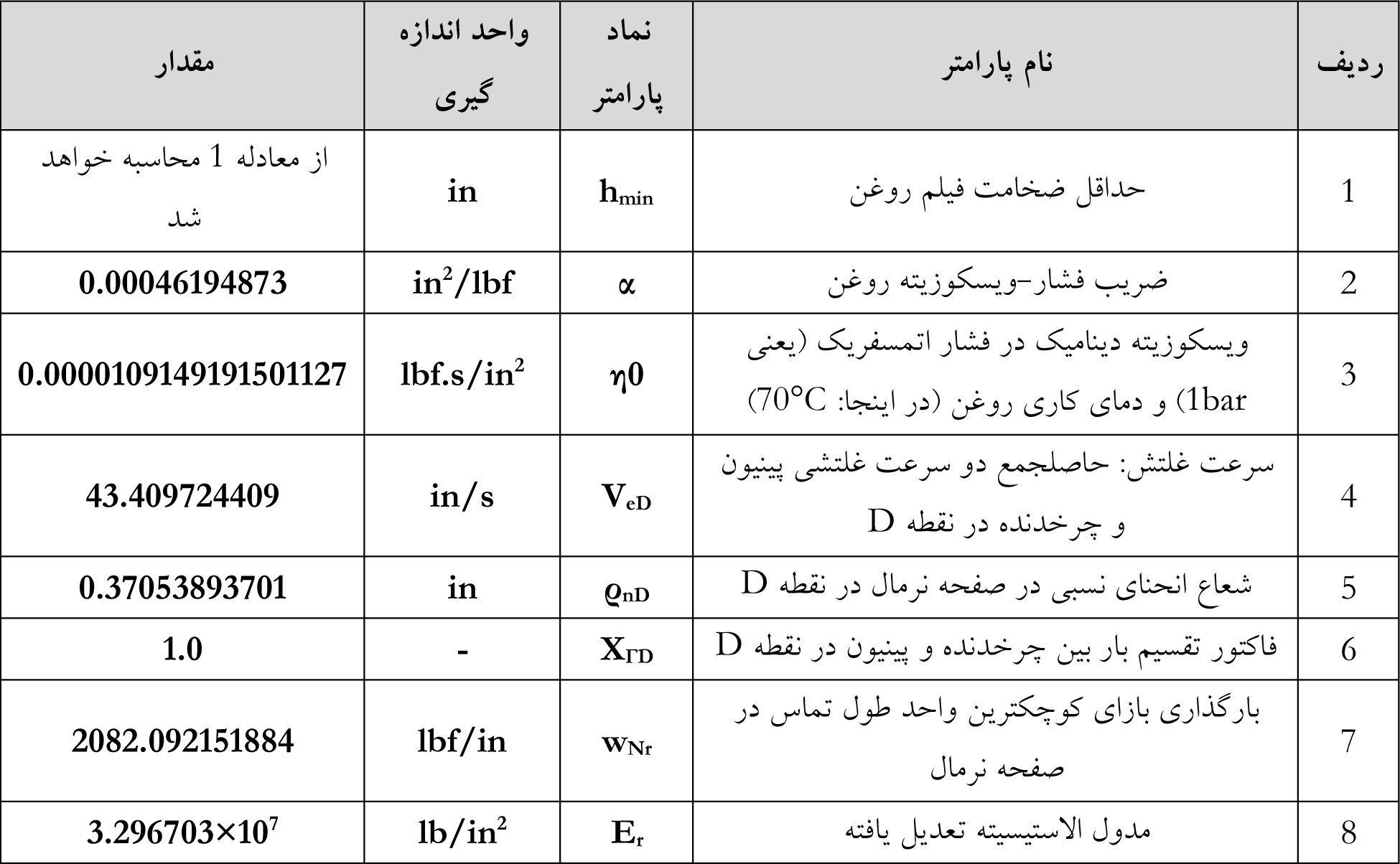
بدین ترتیب، مقدار hmin برحسب mm و in برای روغن فوق در دمای عملکردی فوق برابر خواهد بود با:

حال اگر بخواهیم تاثیر پارامتر η₀ بر h_min را بررسی کنیم، ابتدا باید بازه تغییرات مناسب و معقولی برای η₀ بدست آورده و سپس پاسخ ضابطه h_min را به این تغییرات مدل کنیم. برای اینکار، ابتدا لازمست بازه تغییرات دمایی مناسبی برای η₀ در نظر بگیریم.

در خصوص بازه دمایی، با فرض اینکه دمای کاری محیطی که این گیربکس در آن نصب است (غرب ایران) بین 5 تا 40 درجه سلسیوس است، بنابراین، دمای Cold Start گیربکس را می توان روی +5°C انتخاب کرد. حداکثر دمایی که روغن CLP-PG220 بهران بردبار تحمل خواهد کرد را نیز 100°C فرض می کنیم. چراکه بیش از این عدد دیگر معقول نیست برای روغن های گیربکسی.

پس بدین ترتیب، بازه دمای کاری روغن گیربکس مورد مطالعه در این مقاله +5~100°C فرض می شود.

در ادامه، با فرض فشار اتمسفریک 1bar و با فرض ضریب انبساط حرارتی روغن برابر 0.0007 و معلوم بودن دانسیته روغن در دمای 15°C (شکل 7) می توانیم معادله زیر را برای محاسبه دانسیته روغن در هر دمایی از بازه دمایی فوق بنویسیم:

در معادله 28:

- _Tρ: دانسیته روغن CLP-PG220 بهران در دمای T (بازه تغییرات بین +5 تا 100°C) برحسب gr/cm³؛

- ₁₅ρ: دانسیته روغن فوق در دمای 15°C، برابر با 0.998gr/cm³؛

- a₁₅: ضریب انبساط حرارتی روغن گیربکس فوق که برابر 0.0007 فرض شده است؛ و

- T: دمای کاری روغن بین +5 تا 100°C

در مرحله بعد، برای محاسبه η_T نیازمند آنیم که ویسکوزیته سینماتیک روغن گیربکس را در بازه دمایی که تعریف کرده ایم، بدانیم. در این خصوص، مانند روشی که در ابتدای این مقاله طی کردیم، عمل می کنیم:

در رابطه شماره 29 که قبلا در شکل 6 نشان داده بودیم:

- ν_T: ویسکوزیته سینماتیک روغن در دمای معینی از بازه دمایی 5~100°C؛

- T: دمای کاری روغن برحسب درجه کلوین (بین 278.15~373.15°K)؛

- ضرایب α و β نیز همان مقادیری هستند که قبلا حساب کرده بودیم:

بنابراین، معادله 29 بصورت زیر قابل بازنویسی است:

بدین ترتیب، برای محاسبه η_0T، یعنی «ویسکوزیته دینامیک در دمای کاری روغن» خواهیم داشت:

هرچند، نباید فراموش کرد که برای استفاده از مقدار η_0T بدست آمده از معادله 31 لازمست واحد اندازه گیری از cP به lbf.s/in² تغییر کند.

اکنون، بعنوان مرحله آخر از این بخش از محاسبات، اثر تغییر η_0T را بر h_min می بینیم. از معادله 1 داشتیم:

بدین ترتیب، مقدار h_min برحسب in و mm در هر نقطه ای از بازه دمایی 5~100°C با استفاده از معادله 32 قابل استحصال خواهد بود. جدول 6 را ببینید.

جدول 6: مقادیر محاسبه شده برای h_min براساس تغییرات T و η_0T

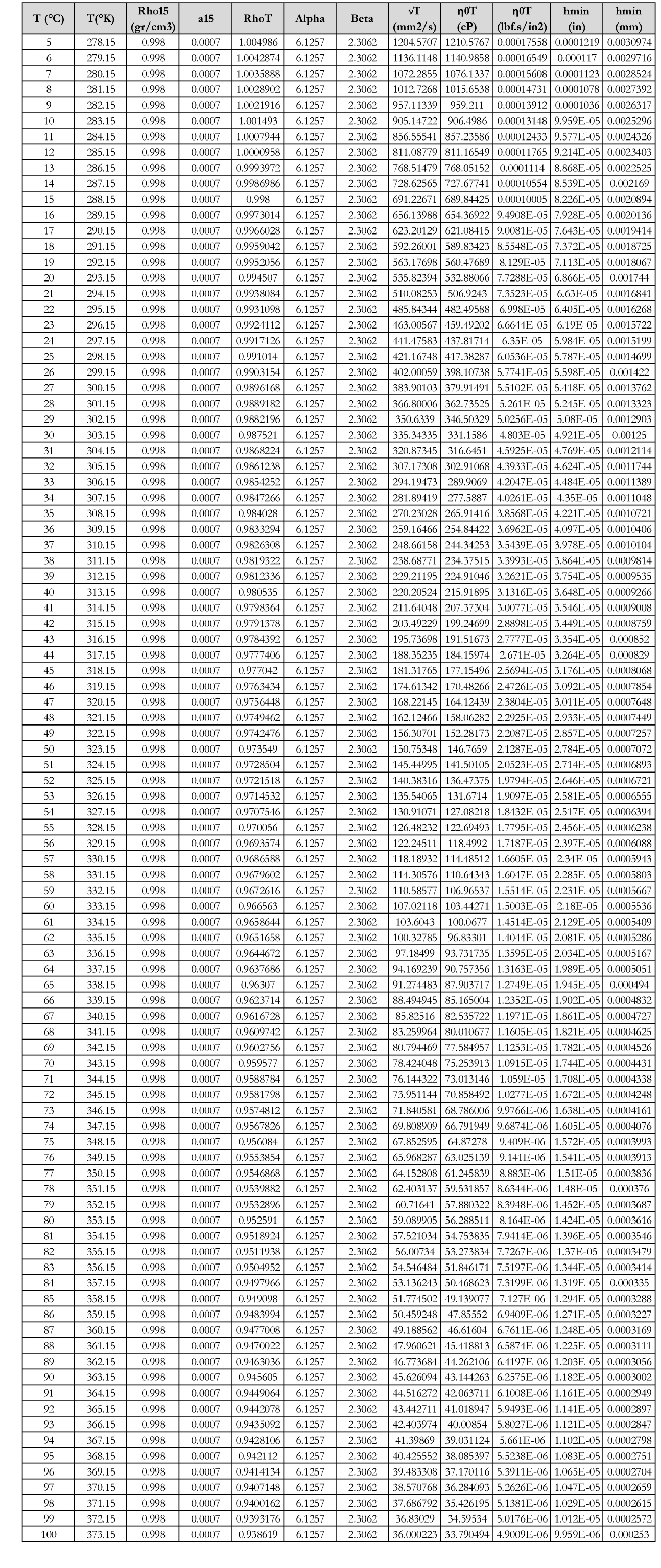
بر همین اساس، حداقل ضخامت فیلم روغن در نقطه D (شکل 12) و در دمای 70°C برابر با 0.4431μm خواهد بود. بنابراین، با توجه به اینکه این عدد در بازه 0.4 تا 0.8 میکرون قرار می گیرد. پس می توان ادعا کرد که چرخدنده و پینیون این گیربکس در دما و در محل تعریف شده با رژیم EHL روغنرسانی می شوند [10,15,19].

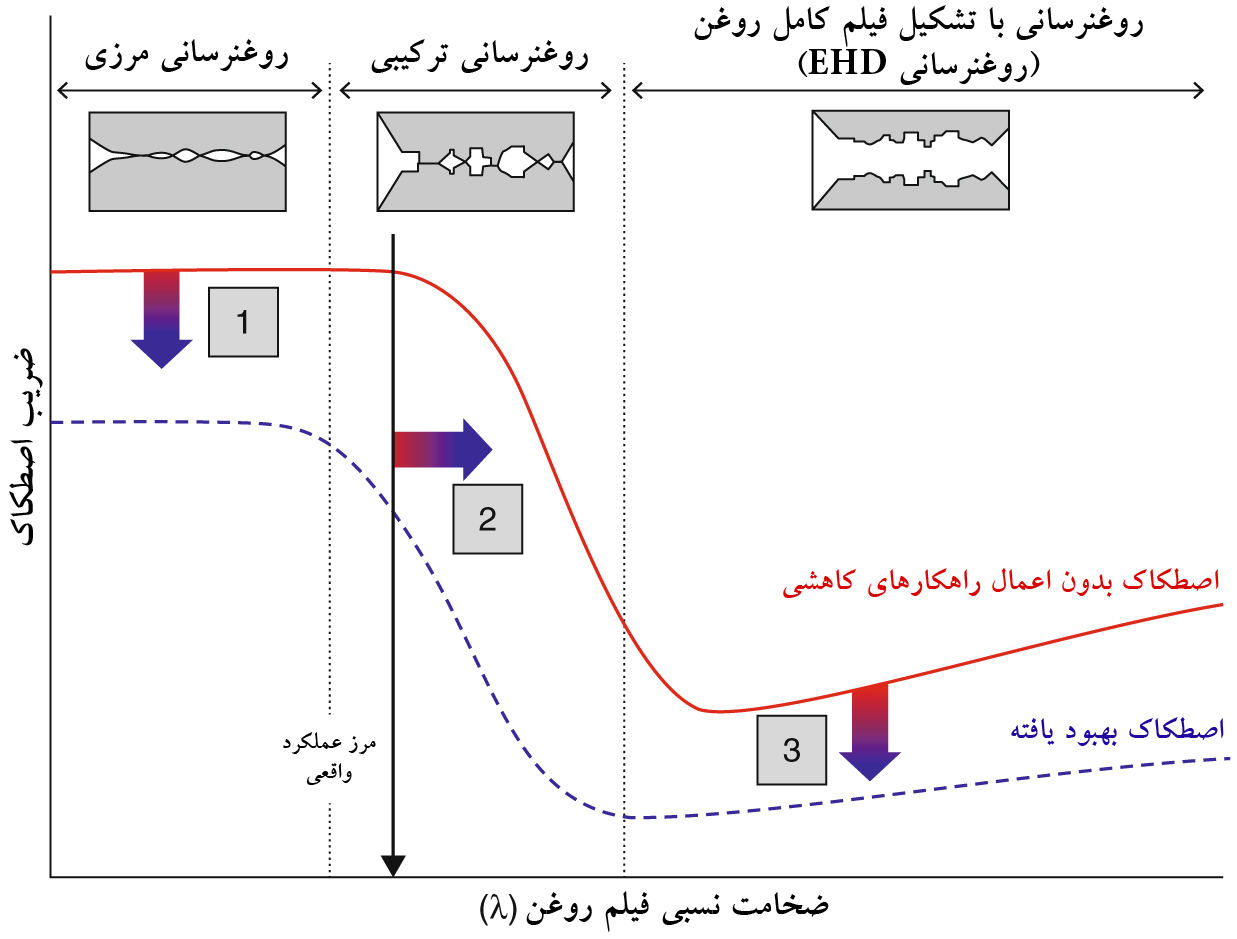
شکل 17: رژیم های روغنرسانی براساس ضخامت فیلم روغن (نمودار Stribeck) [15]

روند تاثیر گذاری تغییرات η_0T بر مقدار h_min که در معادله 32 حاصل شده بود، در شکل 18 نشان داده شده است:

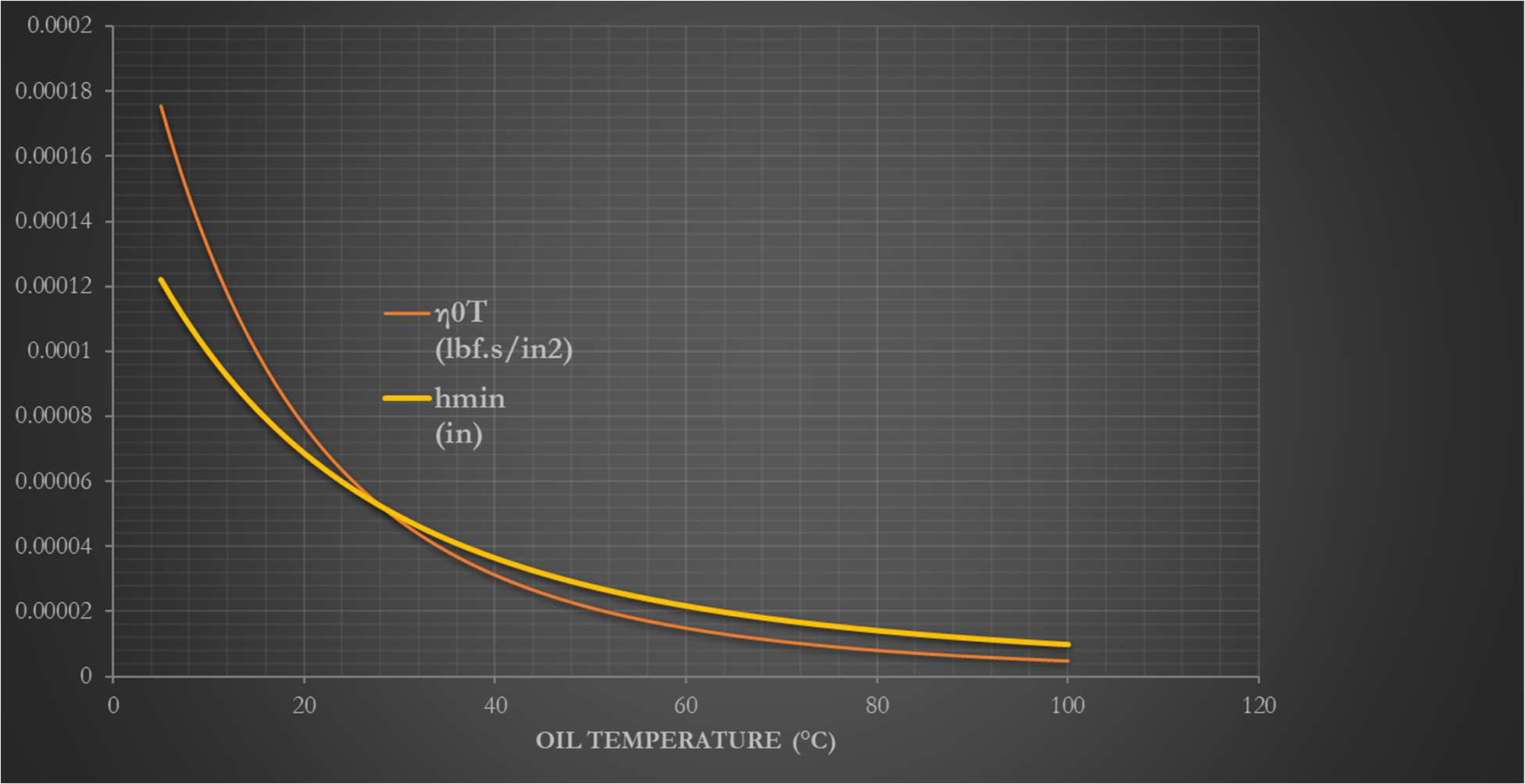
شکل 18: تاثیر تغییرات η_0T در بازه حرارتی 5~100°C روی h_min

همانطور که از نمودار شکل 18 مشهود است، ویسکوزیته دینامیک روغن گیربکس و حساسیت آن به دما (که به ساختار شیمیایی، سلامت روغن، و تنوع و اثربخشی ادتیوهای حاضر در ترکیب شیمیایی آن باز می گردد) تاثیر شدیدی روی حداقل ضخامت فیلم استحصالی از آن روغن دارد. در خصوص نحوه محاسبه ضخامت فیلم روغن و میزان تاثیر پارامترهای مرتبط با کیفیت روغن در مقاله ای جداگانه بحث خواهیم کرد.

بعنوان نتیجه گیری از تمام محاسبات و روابط ریاضی معرفی شده تا بدینجای کار، استفاده از روغن CLP-PG220 بهران برای این جعبه دنده بلامانع بوده است. سازنده یا وندور گیربکس در شکل 3.2 از عبارت CLP یا PGLP برای بیان مشخصات عملکردی یا Performance روغن مصرفی در این گیربکس استفاده کرده است. این مشخصات در جدول 7 با جزییات بیشتری نشان داده شده است.

جدول 7: کلاس های مختلف عملکردی روغن های مناسب برای گیربکس های صنعتی [2,4]

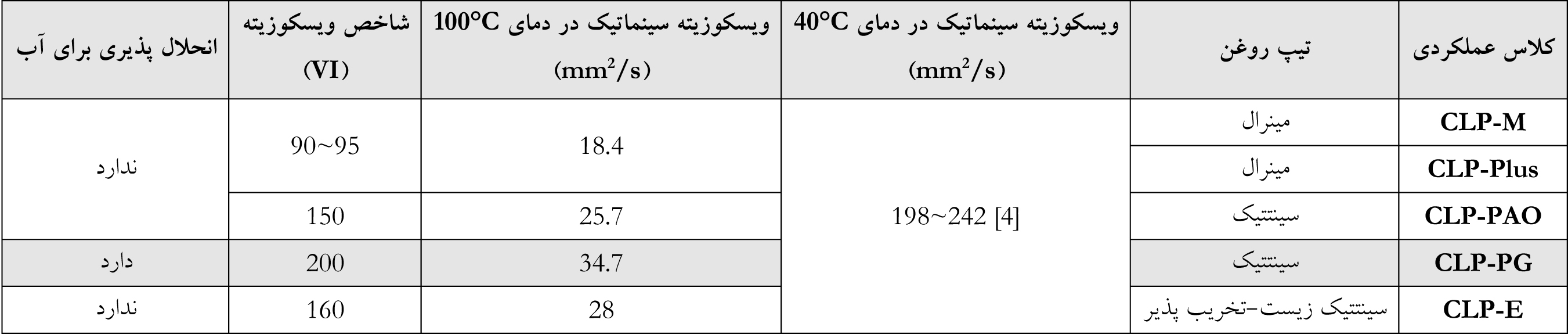
در مورد کلاس های عملکردی نشان داده شده در جدول 7 لازم بذکر می داند که نحوه نمایش کلاس عملکردی روغن های گیربکسی با استفاده از استاندارد DIN 51502 در این جدول نشان داده شده است. اما عبارت CLP دقیقا یعنی چه؟

براساس دو استاندارد DIN 51502  و DIN 51517، عبارت CLP کدی برای بیان مشخصات ساختاری روغن های گیربکسی است که هر حرف از این کد معنی زیر را می دهد:

- حرف C بیانگر الزام به حضور ادتیوهای ضدخوردگی (Anti-Corrosion) در ساختار شیمیایی روغن گیربکسی است (برای اطلاعات بیشتر در خصوص ادتیوهای ضد خوردگی، مراجعه به مقاله «مقدمه ای بر ادتیوهای روغن و گریس: بخش دوم؛ بازدارنده های خوردگی» در همین وبلاگ توصیه می شود)؛

- حرف L بیانگر الزام به حضور ادتیوهای مقاومت به پیرسازی (Aging resistance) در ساختار شیمیایی روغن؛ و

- حرف P نشان دهنده لزوم حضور استفاده از ادتیوهای ضد سایش (Anti-Wear: AW) در فرمولاسیون روغن گیربکسی است [4,5].

بدین ترتیب، و با استناد به مندرجات جدول 7، تمامی روغن های گیربکسی آبگریز هستند، الا PAG.

بنابراین، در بخش بعدی این مقاله لازمست به ساختار روغن های PAG نگاهی دقیق داشته باشیم.

2. روغن های PAG: نگاه نزدیک

روغن های PAG به گروهی از روغن های صنعتی تعلق دارند که در ادبیات مهندسی و روانکاری با عنوان روغن های سینتتیک شناخته شده [23,27] و نزدیک به 24 درصد حجم کل روغن های سینتتیک مصرفی در جهان را شامل می شوند [27].

تحقیق و توسعه فرمولاسیون لازم برای این تیپ از روغن های صنعتی، اما، اصلا چیز جدیدی نیست و به سال های قبل از جنگ جهانی دوم باز می گردد. اولین تلاش های جدی برای ارائه یک فرمولاسیون جدید از روغن های سینتتیک با تحریم دسترسی آلمان ها به منابع نفتی از طریق متفقین و توسط کمپانی I.G. Farben کلید خورد. هرچند، اولین استفاده رسمی از روغن های PAG در روانکاری موتورهای هواپیماهای امریکایی در سال 1944 ثبت شده است. امروزه، اما، عوامل محدودکننده ای چون سقف قیمت تمام شده و تطابق با استانداردهای زیست محیطی باعث شده اند که روغن های PAG مدرن از واکنش بین بوتیلن اکساید با پروپیلن اکساید [27] بمنظور تشکیل یک ساختار شیمیایی برپایه پلی اتر [12] بعنوان پایه بهره جسته و با تکیه بر زنجیره طویلی از الکل های محلول در روغن یا حتی آب [27]، ضمن دستیابی به تطابق لازم با محیط زیست، شاخص ویسکوزیته (VI) بالا و ضریب اصطکاک بسیار پایینی [23,30] را ارائه کنند [23].

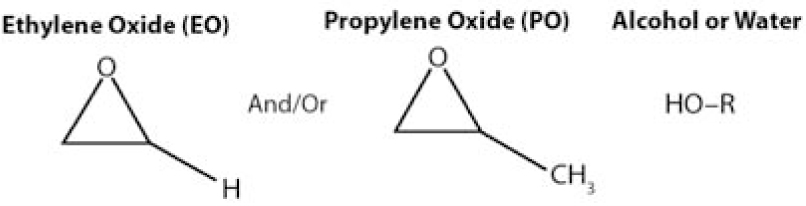
شکل 19: عوامل تشکیل روغن PAG [27]

روغن های گیربکسی PAG دارای VI بالا (اغلب بالاتر از 200، جدول 7 را ببینید)، پایداری حرارتی عالی، و مقاومت بسیار خوب به اکسیداسیون برخوردارند [12,25,30]. همین باعث عمر بیشتر روغن های PAG در مقایسه با دیگر روغن های گیربکسی تیپ مینرال یا سینتتیک می شود. شکل 20 را ببینید.

روغن های PAG حتی تا آخرین لحظات تعویض خود نیز ویسکوزیته خود را در محدوده استاندارد حفظ می کنند. اصولا، نکته جالب در مورد روغن های PAG آنست که تنها تغییری که انقضای عمر روغن را نشان می دهد، عدد اسیدی یا AN است. روغن های PAG نو، بسته به نوع ادتیوهای بکار رفته در ساختار شیمیایی خود، عدد اسیدی 0.1~0.5mgKOH/g را از خود نشان می دهند که این عدد می تواند پس از کارکرد روغن در تجهیز تا سقف 1.0mgKOH/g افزایش پیدا کند [25]. دلیل اصلی این افزایش عدد اسیدی (AN) نیز به آبدوستی روغن PAG برمی گردد. بطوریکه جذب 1000ppm آب در حجم ثابتی از روغن PAG می تواند عدد اسیدی آن را به مراتب افزایش دهد [26].

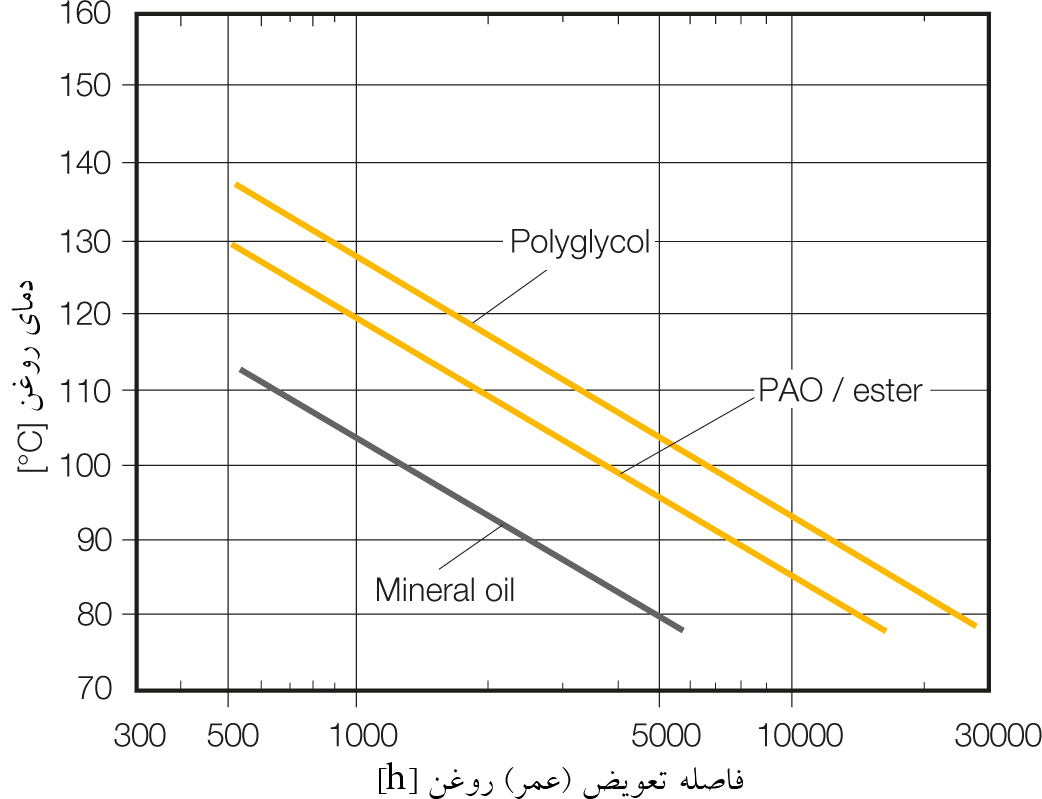
شکل 20: نمودار زمان تعویض روغن برحسب دمای روغن [30]

ولی با اینحال، این تیپ از روغن ها در کنار تمایل به جذب رطوبت بالا بدلیل آبدوستی (Hygroscopicity) [12,26]، نسبت به خوردگی ناشی از آب شور (Salt Water Corrosion) نیز عملکرد ضعیفی داشته و لذا باید در انتخاب این دسته از روغن ها برای روانکاری گیربکس هایی (یا بیان عمومی: تجهیزاتی) که در معرض آب شور یا محیط های پرنمک قرار دارند، با احتیاط عمل کرد. در عین حال، روغن های PAG با اغلب متریال های رایج بکار رفته در انواع واشرها، درزگیرها، رنگ ها، و فیلترها سازگاری نداشته و موجب فساد آنها را در صورت تماس مستقیم فراهم خواهد آورد [12].

از این گذشته، روغن های PAG را نمی توان به سادگی با روغن های مینرال یا دیگر سینتتیک ها ترکیب یا مخلوط کرد [12,25,30]. البته، میزان آبدوستی و میل به ترکیب با سایر روانکارها به نسبت اتیلن اکساید به پلی پروپیلن اکساید در ساختار شیمیایی PAG حاصله بستگی دارد [12]. بطوریکه روغن های PAG با 100 درصد اکسی پروپیلن (PO) در ساختار شیمیایی خود کاملا محلول در آب بوده و از آنسو، آن دسته از PAG هایی که از نسبت EO/PO برابر 75/25 یا 50/50 یا 60/40 در ساختار خود داشته باشند، به همان نسبت، در دمای محیط نسبت به آب تا حدودی نامحلول خواهند بود [25,27].

بطورکلی، از آنجا که روغن های PAG نسبت به انواع روانکارهای مینرال تحمل آب بیشتری دارند، بنابراین، باید در آنالیز این دسته از روغن ها استاندارد سقف وجود آب در نمونه روغن را بسیار بالاتر از انواع مینرال (و حتی سایر سینتتیک ها [28]) گرفت. بطوریکه حتی انواع «نامحلول در آب» روغن های PAG می توانند براحتی حاوی 0.7 درصد وزنی یا حتی 1.0 درصد وزنی (معادل 10,000ppm) [27] آب در ساختار خود (بعنوان آلودگی) باشند [25]. هرچند، از آنجا که این آب در حالت آزاد قرار ندارد (برای اطلاعات بیشتر راجع به آب آزاد، مراجعه به مقاله «تشخیص آلودگی روغن با هوا و آب» توصیه می شود)، پس حضور این مقدار آب در ترکیب PAG نه روی عمر برینگ (بعنوان یکی از اجزای مکانیکی) اثر مخرب داشته و نه تمایل به خوردگی را افزایش می دهد [27]. جدول 8 را ببینید.

جدول 8: مقایسه ای از میزان تقریبی آب حاضر در ترکیب شیمیایی روغن PAG در قیاس با دو روغن PEE [30]

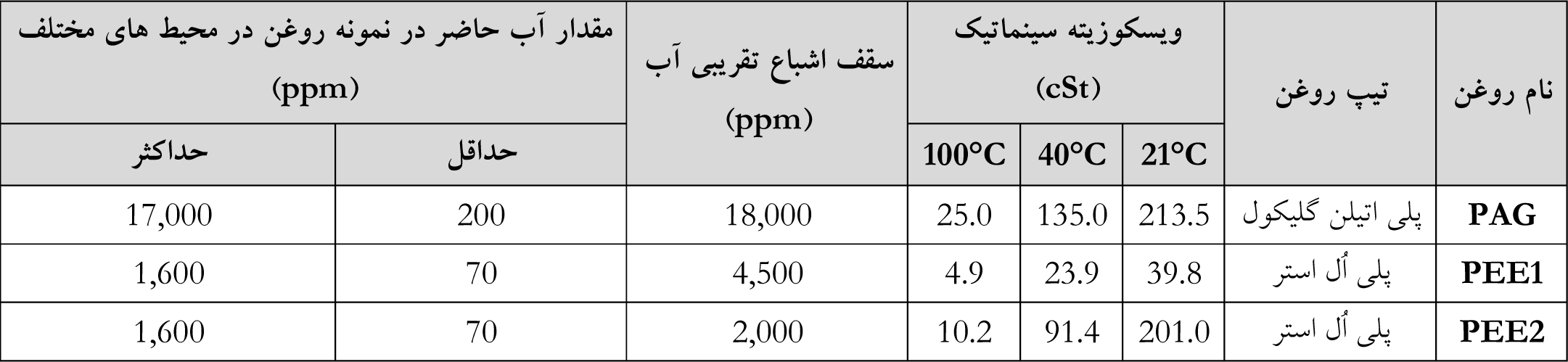
بنابراین، همانطور که در جدول 8 نیز دیده می شود، مقدار 17,000ppm آب خوانده شده در نتیجه تست نمونه روغن بهران بردبار PG220 موضوع مطالعه این مقاله اصلا چیز عجیبی نیست و کاملا تعریف شده و نرمال است.

3. نتیجه گیری

روغن بهران بردبار PG220 برای این گیربکس که در دمای 70°C نیز از رژیم روغنرسانی EHL پیروی می کند بمنظور روغنرسانی به چرخدنده ها، انتخاب خوبیست و کیفیت مناسبی نیز دارد. بطوریکه حداقل ضخامت لازم برای دستیابی و حفظ فیلم روغن در دمای 70°C را کاملا تامین می کند. مقدار آب 17,000ppm خوانده شده در نتایج تست نیز با توجه به ساختار شیمیایی روغن های PAG و عدم آزاد بودن آب، موضوعی کاملا طبیعی بوده و برای گیربکس خطری ندارد. هرچند، توصیه می شود جهت پایش سلامت و وضعیت این روغن و این گیربکس تست عدد اسیدی (AN) و pH مطابق روال بیان شده در مقاله «عدد اسیدی، عدد قلیایی، و pH روغن» انجام شده و نتایج با حدود مجاز درج شده در بند 2 این مقاله مقایسه گردد تا از بروز خسارت به تجهیز جلوگیری شود.

4. منابع و مآخذ

در نگارش این مقاله، علاوه بر تجربیات و مشاهدات شخصی، از منابع زیر نیز بهره برداری شده است که فهرست کوتاهی از آنها جهت مطالعه بیشتر خوانندگان محترم در این حوزه به شرح زیر تقدیم شده است:

1. Kohara Gear Industry Co. Ltd., Lubrication of Gears, Web Article, available at https://khkgears.net/new/gear_knowledge/gear_technical_reference/lubrication-of-gears.html, accessed at Feb., 12^th, 2021;

2. T. Mang, W. Dresel (Editors), Lubricants & Lubrication, 2^nd ed., Wiley-VCH, ISBN 978-3-527-31497-3, 2007, pp77-79, pp230-273;

3. W. F. Navarro, Viscosity @ Temperature, WEG-CESTARI, LinkedIn article, https://www.linkedin.com/pulse/viscosity-temperature-walmir-fernandes-navarro/, Published at April 8^th 2019, e-mail: [e-mail];

4. DIN 51517-3-2014, Schmierstoffe- Schmieröle- Teil 3: Schmieröle CLP, Mindestanforderungen, Alleinverkauf der Normen durch Beuth Verlag GmbH, Burggrafenstraße 6, 1000 Berlin 30, Deutschland;

5. DIN 51502-1990, Schmierstoffe und verwandte Stoffe; Kurzbezeichnung der Schmierstoffe und Kennzeichnung der Schmierstoffbehälter, Schmiergeräte und Schmierstellen, Alleinverkauf der Normen durch Beuth Verlag GmbH, Burggrafenstraße 6, 1000 Berlin 30, Deutschland;

6. R. Errichello, The Lubrication of Gears – Part 1, GEAR TECHNOLOGY, March/April 1991, pp18-26, http://www.geartechnology.com;

7. R. Errichello, The Lubrication of Gears – Part II, GEAR TECHNOLOGY, May/June 1991, pp18-22, http://www.geartechnology.com;

8. T. L. Krantz, On the Correlation of Specific Film Thickness and Gear Pitting Life, GEAR TECHNOLOGY, January/February 2015, pp52-62, http://www.geartechnology.com;

9. J. Michaud, Lambda Ratio: Surface roughness must be accurately characterized in order for the lambda ratio to be a completely effective tool, published at October 14, 2016, Web Article, Available at https://gearsolutions.com/departments/materials-matter-lambda-ratio/, accessed at February 16, 2021;

10. Noria Corporation, Lubrication Regimes Explained, Web Article, Available at https://www.machinerylubrication.com/Read/30741/lubrication-regimes, accessed at February 19, 2021;

11. E. J. Wellauer, G. A. Holloway, Application of EHD film Theory to Industrial Gear Drives, Journal of Engineering for Industry, ASME, May 1976, 98(2), pp626-631, DOI: https://doi.org/10.1115/1.3438951;

12. ISO/TR 18792:2008(E), Lubrication of industrial gear drives, International Organization for Standardization, Case postale 56 • CH-1211 Geneva 20;

13. Q. J. Wang, Y. W. Chung (Editors), Encyclopedia of Tribology, Springer Reference, 2013, ISBN: 978-0-387-92897-5, DOI: 10.1007/978-0-387-92897-5, pp832-847, p1286;

14. AGMA 925-A03, Effect of Lubrication on Gear Surface Distress, American Gear Manufacturers Association, 2003, ISBN: 1-55589-815-7;

15. J. Amendola, J. Amendola III, and R. Errichello, Calculated Scuffing Risk: Correlating AGMA 925-A03, AGMA 6011-J14 and Original MAAG Gear Predictions, GEAR TECHNOLOGY, March/April 2020, pp50-57, http://www.geartechnology.com;

16. M. Marian, M. Bartz, S. Wartzack, and A. Rosenkranz, Non-Dimensional Groups, Film Thickness Equations and Correction Factors for Elastohydrodynamic Lubrication: A Review, Lubricants 2020, 8, 95, doi:10.3390/lubricants8100095, http://www.mdpi.com/journal/lubricants;

17. G. Nijenbanning, C. H. Venner, and H. Moes, Film thickness in elastohydrodynamically lubricated elliptic contacts, Wear 176 (1994) 217-229, Elsevier Science S.A., 1994, https://doi.org/10.1016/0043-1648(94)90150-3;

18. R. Errichello, Selecting Oils with High Pressure-Viscosity Coefficient, Machinery Lubrication, 3/2004;

19. AGMA 9005-D94, Industrial Gear Lubrication, American Gear Manufacturers Association, 1994, ISBN: 1-55589-632-4;

20. A. Adebogun, R. Hudson, A. Matthews, and P. J. Withers, Industrial Gear Oils: Influence of Bulk Oil Temperature and Contact Pressure on Tribological Performance and Subsurface Changes, Tribology Letters (2020) 68:48, Springer, March 2020, DOI: https://doi.org/10.1007/s11249-020-1287-z;

21. Boston Gear, Engineering Information; Spur Gears: Gear Nomenclature, P-1930-BG 4/20, p307, http://www.bostongear.com;

22. J. Davis (Editor), Gear Martials, Properties, and Manufacture, ASM International, Chapter 2: Gear Tribology and Lubrication, pp19-38, 2005, ISBN: 0-87170-815-9;

23. R. Shah (on behalf of Koehler Instrument Company), Synthetic Lubricants and Their Long-Term Efficiency and Sustainability, published at February 11, 2021, Web Article, Available at https://www.petro-online.com/article/biofuel-industry-news/22/koehler-instrument-company/synthetic-lubricants-and-their-long-term-efficiency-and-sustainability/2893, accessed at March 11, 2021;

24. ANSI/AGMA 2101-D04, Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth, American Gear Manufacturers Association, pp12-17, 2004, ISBN: 1-55589-840-8;

25. D. Bearty, M. Greaves, PAGs are Rising to the Top of the Synthetic Market, Machinery Lubrication, September/October 2006, pp36-40, http://www.machinerylubrication.com;

26. WAECO, Why PAG oils have to be protected against moisture, Special report air conditioning know‐how, Web Article, available at https://www.waeco.com/en/de/news/why-pag-oils-have-to-be-protected-against-moisture, accessed at Feb., 12^th, 2021;

27. W. Escobar, Understanding Ployalkylene Glycoles & Where to Apply Them, Tribology and Lubrication Technology (TLT), May 2008, pp34-39, http://www.stle.org;

28. W. H. Van Glabbeek, T. K. Sheiretov and C. Cusano, The Effect of Dissolved Water on the Tribological Properties of Polyalkylene Glycol and Polyolester Oils, Prepared as part of ACRC Project 04 Compressor--Lubrication, Friction, and Wear, ACRCTR-70, Air Conditioning and Refrigeration Center, University of Illinois, Mechanical & Industrial Engineering Dept., Nov. 1994;

29. R. Errichello, Selecting Oils with High Pressure-Viscosity Coefficient, Machinery Lubrication, 3/2004, http://www.machinerylubrication.com;

30. Klüber Lubrication, Gear oils made by Klüber Lubrication, B023001002 / Edition 11.15, Klüber Lubrication München SE & Co. KG, http://www.klueber.com.